Минимизация функций алгебры логики
Общая задача минимизации булевых функций может быть сформулирована таким образом: найти аналитическое выражение заданной булевой функции в форме, содержащей минимальное число букв. Эта задача достаточно хорошо исследована в классе дизъюнктивно – конъюнктивных форм.
Определение: Минимальной ДНФ булевой функции называется ДНФ, содержащая наименьшее число букв по отношению к другим ДНФ, представляющим заданную булеву функцию.
Определение: Булева функция q(x1… xn) называется импликантой булевой функции f(x1… xn) если для любого набора переменных, на котором 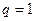 , справедливо
, справедливо 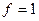 .
.
Определение: Импликанта 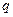 булевой функции
булевой функции 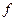 , являющаяся элементарной конъюнкцией, называется простой, если никакая часть импликанты
, являющаяся элементарной конъюнкцией, называется простой, если никакая часть импликанты 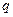 не является импликантой функции
не является импликантой функции 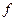 .
.
1. Дизъюнкция любого числа импликант булевой функции 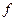 так же является импликантой этой функции.
так же является импликантой этой функции.
2. Любая булева функция 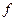 эквивалентна дизъюнкции всех своих простых импликант. Такая форма называется сокращенной ДНФ.
эквивалентна дизъюнкции всех своих простых импликант. Такая форма называется сокращенной ДНФ.
Пример:
| x1 | x2 | x3 | f | q1 | q2 | q3 | q4 | q5 | q6 | q7 |
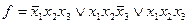
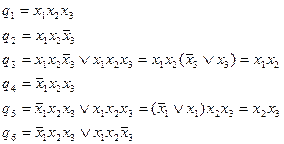
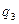 и
и 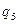 простые импликанты.
простые импликанты.
Сокращенная ДНФ 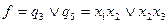 :
:
Импликанты 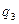 и
и 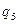 покрывают своими "1" все "1" функции
покрывают своими "1" все "1" функции 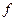 .
.
Получение сокращенной ДНФ является первым этапом отыскания минимальных форм булевых функций. Иногда из СкДНФ можно убрать одну или несколько простых импликант, не нарушая эквивалентности исходной функции. Такие простые импликанты называются лишними. Их исключение из СкДНФ – второй этап минимизации.
Определение: СкДНФ булевой функции называется тупиковой, если в ней отсутствуют лишние простые импликанты.
Тупиковые ДНФ булевых функций 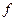 , содержащие минимальное число букв, являются минимальными. МДНФ может быть несколько.
, содержащие минимальное число букв, являются минимальными. МДНФ может быть несколько.
Метод Квайна
Метод применим к СДНФ и основывается на применении двух основных соотношений:
1. склеивание 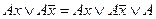
2. поглощение 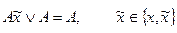
Суть метода заключается в последовательном выполнении всех возможных склеиваний и затем всех поглощений, что приводит к СкДНФ.
Для получения МДНФ необходимо убрать из СкДНФ все лишние простые импликанты с помощью импликантной матрицы Квайна. В строках матрицы отмечаются простые импликанты, а в столбцах – конституэнты "1" булевой функции. Минимальные ДНФ строятся по импликантной матрице таким образом:
1) ищутся столбцы матрицы, имеющие только один крестик. Соответствующие этим крестикам простые импликанты называются базисными и составляют ядро булевой функции. Ядро обязательно входит в МДНФ.
2) рассматриваются различные варианты выбора совокупности простых импликант, которые накроют крестиками остальные столбцы матрицы, и выбираются варианты с минимальным суммарным числом букв в такой совокупности импликант.
Пример: 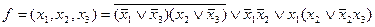 .
.
1) Избавимся от отрицаний и скобок: 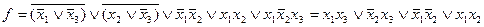
2) Восстановим СДНФ, применяя развертывание:
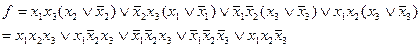
3) Найдем СкДНФ, произведя все возможные склеивания:
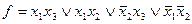
4) Ищем МДНФ:
 |
Ядро: 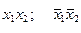
МДНФ: 
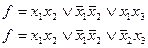
Дата добавления: 2016-07-18; просмотров: 2994;











