Системы функций алгебры логики
Любая булева функция может быть представлена одной из НФ. Эти формы используют ограниченное число элементарных булевых функций.
Например: для СДНФ такие функции 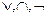 .
.
Следовательно, существуют системы ФАЛ с помощью которых можно аналитически представить любую сколь угодно сложную булеву функцию. Проектирование ЦА основано на знании таких систем ФАЛ из которых можно построить произвольный ЦА.
Базисом, функционально полной системой булевых функций (ФПСБФ) называют совокупность таких булевых функций 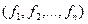 , что произвольная ФАЛ
, что произвольная ФАЛ 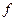 может быть записана в виде формулы через функции этой совокупности.
может быть записана в виде формулы через функции этой совокупности.
ФПСБФ: 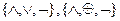
Определим свойства, которыми должна обладать функция, составляющие ФПСБФ. Рассмотрим предполные классы ФАЛ. Проведённые исследования показали, что предполных классов – 5, а для построения ФПСБФ необходимо и достаточно, чтобы её функции не содержались полностью ни в одном из 5 предполных классов.
Предполные классы ФАЛ:
1. класс функций, сохраняющих const 0
2. класс функций, сохраняющих const 1
3. класс самодвойственных булевых функций
4. класс линейных булевых функций
5. класс монотонных булевых функций
Функции класса 2. Если функция на единичном наборе = 1, то говорят, что она сохраняет единицу 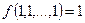 .
.
Функция класса 1. – 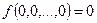 .
.
Функции класса 3. ФАЛ называют самодвойственной, если на каждой паре противоположных наборов она принимает противоположные значения, то есть
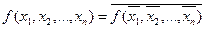
Функции класса 4. К линейным ФАЛ относятся функции, которые могут представить в виде 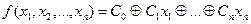 , где
, где 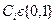 .
.
Функции класса 5. ФАЛ называют монотонной, если при любом возрастании набора значения этой функции не убывают.
Теорема Поста-Яблонского. Для того, чтобы система ФАЛ была функционально полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию:
- не сохраняющую 0,
- не сохраняющую 1,
- не являющуюся линейной,
- немонотонную,
- не самодвойственную.
Рассмотрим примеры ФПСБФ:
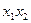
| Функция | классы | |||||||
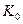
| 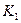
| 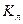
| 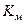
| 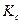
| |||||
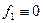
| 
| 
| 
| ||||||
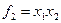
| 
| 
| 
| ||||||
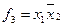
| 
| ||||||||
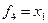
| 
| 
| 
| 
| 
| ||||
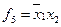
| 
| ||||||||
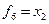
| 
| 
| 
| 
| |||||
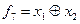
| 
| 
| |||||||
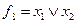
| 
| 
| 
| ||||||
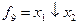
| + | + | + | + | + | ||||
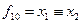
| 
| 
| |||||||
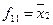
| 
| 
| |||||||
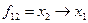
| 
| ||||||||
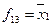
| 
| 
| |||||||
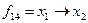
| 
| ||||||||
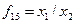
| + | + | + | + | + | ||||
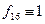
| 
|
Функции 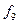 и
и 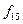 являются ФПСБФ. Из таблицы можно получить и другие ФПСБФ:
являются ФПСБФ. Из таблицы можно получить и другие ФПСБФ: 
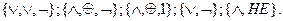
Дата добавления: 2016-07-18; просмотров: 2225;











