Совершенные нормальные формы
НКФ и НДФ не дают однозначного представления функции. Такое представление получается только при совершенных НФ.
СНДФ – ФАЛ, заданная в виде: 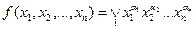 , где
, где 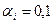 и
и
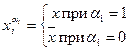 .
.
Основные свойства СНДФ:
- В СНДФ нет двух одинаковых минтермов;
- В СНДФ ни один минтерм не содержит двух одинаковых множителей (переменных);
- В СНДФ ни один минтерм не содержит вместе с переменной и её отрицание.
Выписывать в СНДФ имеет смысл только конституэнты 1, соответствующие единичным наборам функции.
Любая ФАЛ, кроме абсолютно истинной функции, может быть представлена в СНДФ: 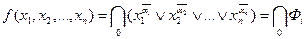
Пример: Функция задана таблицей истинности.
Представим ее в СНДФ и СНКФ.
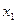
| 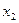
| 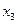
| 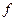
|
СДНФ: 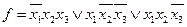
СКНФ: 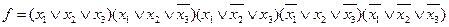
Способы преобразования НФ в СНФ. СНФ отличается от НФ тем, что содержит термы максимального ранга и даёт однозначное представление функции.
Произвольная НДФ переводится в СДНФ таким образом:
Пусть 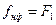 , тогда
, тогда 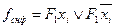 , где
, где 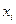 – переменная, которая не входит в данный терм.
– переменная, которая не входит в данный терм.
Пример: Преобразовать ФАЛ в СДНФ:
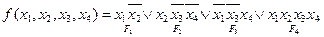
Произвольная НКФ переводится в СКНФ таким образом, пусть 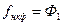 , тогда
, тогда
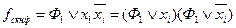
Дата добавления: 2016-07-18; просмотров: 2533;











