Числовые характеристики
Понятие математического ожидания М (Х) и дисперсии D(X) введенные ранее дискретной случайной величины, можно распространить на непрерывные случайные величины.
· Математическое ожидание М (Х) непрерывной случайной величины Х определяются равенством:
+∞
M(X)= ∫ x•f(x)dx,
-∞
при условии, что этот интеграл сходится абсолютно.
· Дисперсия D(X) непрерывной случайной величины Х определяется равенством:
+∞
D(X)= ∫ (х-М(х)2)•f(x)dx, или
-∞
+∞
D(X)= ∫ х2•f(x)dx- (М(х))2
-∞
· Среднее квадратическое отклонение σ(Х) непрерывной случайной величины определяется равенством:
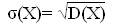
Все свойства математического ожидания и дисперсии, рассмотренные ранее для дисперсных случайных величин, справедливы и для непрерывных.
Задача №3.Случайная величина Х задана дифференциальной функцией f(x):
 0 при х≤0,
0 при х≤0,
f(х)= х/3 при 0<х≤2,
1/3 при 2<х≤3,
0 при х>3.
Найти M(X),D(X),σ(Х), а также P(1<х<5)
Решение
+∞ 0 2 2 +∞ 2 3
M(X)= ∫ х•f(x)dx=∫ х•0dx+∫ х•х/3 dx+∫ х/3dx+∫ 0•х•dx=1/3∫х2dx+1/3∫ хdx=

 -∞ 0 3 2 3 0 3 3 0 2
-∞ 0 3 2 3 0 3 3 0 2
= x3/9 + х2/6 = 8/9-0+9/6-4/6=31/18,
2 2

 +∞ 2 3 2 3
+∞ 2 3 2 3
D(X)= ∫ х2• f(x)dx-(М(х))2=∫ х2•х/3•dx+∫1/3х2 dx=(31/18)2=х4/12 +х3/9 -
-∞ 0 2 0 2
- (31/18)2=16/12-0+27/9-8/9-(31/18)2=31/9- (31/18)2==31/9(1-31/36)=155/324,
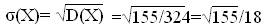

 5 2 3 5 2 3
5 2 3 5 2 3
P(1<х<5)= ∫ f(x)dx=∫ х/3 dx+∫ 1/3 dx+∫ 0 dx= х2/6 +1/3х =
1 1 2 3 1 2
= 4/6-1/6+1-2/3=5/6.
Дата добавления: 2016-07-18; просмотров: 2897;











