Равномерный закон распределения
Определение:Непрерывная случайная величина Х имеет равномерный закон распределения на некотором интервале (а;b), которому принадлежат все возможные значения Х, если плотность распределения вероятностей f(x) постоянная на этом интервале и равна 0 вне его, т.е.
 0 при х≤а,
0 при х≤а,
f(х)= 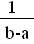 при a<х<b,
при a<х<b,
0 при х≥b .
График функции f(x) изображен на рис. 1
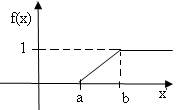
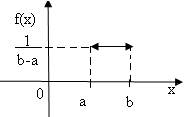 (рис. 1) (рис.2)
(рис. 1) (рис.2)
Функция распределения случайной величины Х, распределенной по равномерному закону, задается формулой:
 0 при х≤а,
0 при х≤а,
F(х)= 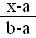 при a<х≤b,
при a<х≤b,
0 при х>b.
Ее график изображен на рис. 2.
Числовые характеристики случайной величины равномерно распределенной на интервале (a;b), вычисляются по формулам:
M(Х)= 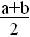 , D(X)=
, D(X)= 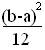 , σ(Х)=
, σ(Х)= 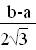 .
.
Задача№1.Случайная величина Х равномерно распределена на отрезке [3;7]. Найти:
а) плотность распределения вероятностей f(x) и построить ее график;
б) функцию распределения F(x) и построить ее график;
в) M(X),D(X), σ(Х).
Решение: Воспользовавшись формулами, рассмотренными выше, при а=3, b=7, находим:
 0 при х<3,
0 при х<3,
а) f(х)= 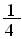 при 3≤х≤7,
при 3≤х≤7,
0 при х>7
Построим ее график (рис.3):
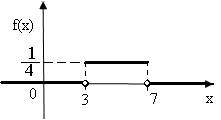 рис.3
рис.3
б)  0 при х≤3,
0 при х≤3,
F(х)= 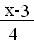 при 3<х≤7,
при 3<х≤7,
1 при х>7 .
Построим ее график (рис.4):
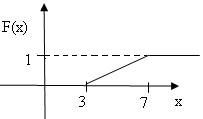 рис.4
рис.4
в) M(X) = 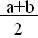 =
= 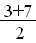 =5,
=5,
D(X) = 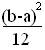 =
= 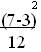 =
= 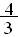 ,
,
σ (Х) = 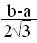 =
= 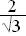 =
= 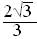 .
.
Дата добавления: 2016-07-18; просмотров: 2352;











