Задачи для самостоятельной работы.
1.1Дисперсная случайная величина Х задана законом распределения:
| х | -2 | |||
| р | 0,3 | 0,2 | Р3 | 0,1 |
Найти р4, функцию распределения F(X) и построить ее график, а также M(X),D(X), σ(Х).
1.2.Дисперсная случайная величина Х задана законом распределения:
| х | -1 | ||||
| р | 0,3 | 0,1 | 0,2 | Р4 | 0,3 |
Найти р4, функцию распределения F(X) и построить ее график, а также M(X),D(X), σ(Х).
1.3. В коробке 9 фломастеров, из которых 2 фломастера уже не пишут. Наудачу берут 3 фломастера. Случайная величина Х- число пишущих фломастеров среди взятых. Составить закон распределения случайной величины.
1.4.На стеллаже библиотеки в случайном порядке расставлено 6 учебников, причем 4 из них в переплете. Библиотекарь берет наудачу 4 учебника. Случайная величина Х-число учебников в переплете среди взятых. Составить закон распределения случайной величины.
1.5.В билете две задачи. Вероятность правильного решения первой задачи равна 0,9, второй-0,7. Случайная величина Х- число правильно решенных задач в билете. Составить закон распределения, вычислить математическое ожидание и дисперсию этой случайной величины, а также найти функцию распределения F(x) и построить ее график.
1.6. Три стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,5, для второго-0,8, для третьего -0,7. Случайная величина Х- число попаданий в мишень, если стрелки делают по одному выстрелу. Найти закон распределения, M(X),D(X).
1.7. Баскетболист бросает мяч в корзину с вероятностью попадания при каждом броске 0,8. За каждое попадание он получает 10 очков, а в случае промаха очки ему не начисляют. Составить закон распределения случайной величины Х-числа очков, полученных баскетболистом за 3 броска. Найти M(X),D(X), а также вероятность того, что он получит более 10 очков.
1.8.На карточках написаны буквы, всего 5 гласных и 3 согласных. Наугад выбирают 3 карточки, причем каждый раз взятую карточку возвращают назад. Случайная величина Х-число гласных букв среди взятых. Составить закон распределения и найти M(X),D(X),σ(Х).
1.9.В среднем по 60% договоров страховая компания выплачивает страховые суммы в связи с наступлением страхового случая. Составить закон распределения случайной величины Х- числа договоров, по которым была выплачена страховая сумма среди наудачу отобранных четырех договоров. Найти числовые характеристики этой величины.
1.10.Радиостанция через определенные промежутки времени посылает позывные сигналы (не более четырех) до установления двусторонней связи. Вероятность получения ответа на позывной сигнал равна 0,3. Случайная величина Х-число посланных позывных сигналов. Составить закон распределения и найти F(x).
1.11.Имеется 3 ключа, из которых только один подходит к замку. Составить закон распределения случайной величины Х-числа попыток открывания замка, если испробованный ключ в последующих попытках не участвует. Найти M(X),D(X).
1.12.Производятся последовательные независимые испытания трех приборов на надежность. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался надежным. Вероятность выдержать испытание для каждого прибора равна 0,9. Составить закон распределения случайной величины Х-числа испытанных приборов.
1.13.Дискретная случайная величина Х имеет три возможные значения: х1=1, х2,х3, причем х1<х2<х3. Вероятность того, что Х примет значения х1 и х2, соответственно равны 0,3 и 0,2. Известно, что М(Х)=2,2, D(X)=0,76. Составить закон распределения случайной величины.
1.14.Блок электронного устройства содержит 100 одинаковых элементов. Вероятность отказа каждого элемента в течении времени Т равна 0,002. Элементы работают независимо. Найти вероятность того, что за время Т откажет не более двух элементов.
1.15.Учебник издан тиражом 50000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0002. Найти вероятность того, что тираж содержит:
а) четыре бракованные книги,
б) менее двух бракованных книг.
1.16.Число вызовов, поступающих на АТС каждую минуту, распределено по закону Пуассона с параметром λ=1,5. Найдите вероятность того, что за минуту поступит:
а) два вызова;
б)хотя бы один вызов.
1.17.Даны законы распределения двух независимых случайных величин:
| х | -2 | ||
| р | 0,5 | 0,2 | 0,3 |
| х | |||
| р | 0,2 | 0,5 | 0,3 |
Х: Y:
Найти M(Z),D(Z), если Z=3X+Y.
1.18.Даны законы распределения двух независимых случайных величин:
| х | |||
| р | 0,1 | 0,4 | 0,5 |
| х | |||
| р | 0,2 | 0,4 | 0,4 |
Х: Y:
Найти M(Z),D(Z), если Z=X+2Y.
Ответы:
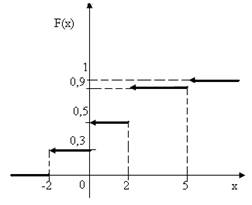

 1.1.р3=0,4; 0 при х≤-2,
1.1.р3=0,4; 0 при х≤-2,
0,3 при -2<х≤0,
F(x)= 0,5 при 0<х≤2,
0,9 при 2<х≤5,
1 при х>5

M(Х)=0,7; D(Х)=4,87; σ(Х) ≈2,193.
 |
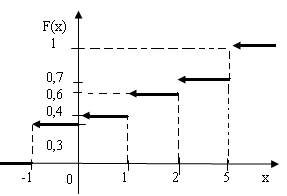 1.2. р4=0,1; 0 при х≤-1,
1.2. р4=0,1; 0 при х≤-1,
0,3 при -1<х≤0,
0,4 при 0<х≤1,
F(x)= 0,6 при 1<х≤2,
0,7 при 2<х≤3,
1 при х>3
 |
M(Х)=1; D(Х)=2,6; σ(Х) ≈1,612.
1.3.
| х | |||
| р | 7/84 | 1/2 | 35/84 |
1.4.
| х | |||
| р | 2/5 | 8/15 | 1/15 |
1.5.
| х | |||
| р | 0,03 | 0,34 | 0,63 |
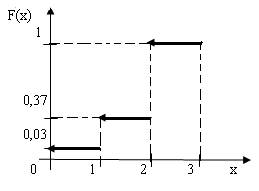

 0 при х≤0,
0 при х≤0,
0,03 при 0<х≤1,
F(x)= 0,37 при 1<х≤2,
1 при х>2
 |
1.6.
| х | ||||
| р | 0,03 | 0,22 | 0,47 | 0,28 |
M(Х)=2; D(Х)=0,62
1.7.
| х | ||||
| р | 0,008 | 0,096 | 0,384 | 0,512 |
M(Х)=2,4; D(Х)=0,48, P(X>10)=0,896
1.8.
| х | ||||
| р | 27/512 | 135/512 | 225/512 | 125/512 |
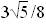 M(Х)=15/8; D(Х)=45/64; σ(Х) ≈
M(Х)=15/8; D(Х)=45/64; σ(Х) ≈
1.9.
| х | |||||
| р | 0,0256 | 0,1536 | 0,3456 | 0,3456 | 0,1296 |
M(Х)=2,4; D(Х)=0,96
1.10.
| х | ||||
| р | 0,3 | 0,21 | 0,147 | 0,343 |

 0 при х≤ 1,
0 при х≤ 1,
0,3 при 1<х≤2,
F(x)= 0,51 при 2<х≤3,
0,657 при 3<х≤4,
1 при х>4
 1.11.
1.11.
| х | |||
| р | 1/3 | 1/3 | 1/3 |
M(Х)=2; D(Х)=2/3
1.12.
| х | |||
| р | 0,9 | 0,09 | 0,01 |
1.13.
| х | |||
| р | 0,3 | 0,2 | 0,5 |
1.14.1,22• e-0,2≈0,999
1.15. а)0,0189; б) 0,00049
1.16. а)0,0702; б)0,77687
1.17. 3,8; 14,2
1.18. 11,2; 4.
Глава 2. Непрерывная случайная величина
Определение: Непрерывной называют величину, все возможные значения которой полностью заполняют конечный или бесконечный промежуток числовой оси.
Очевидно, число возможных значений непрерывной случайной величины бесконечно.
Непрерывную случайную величину можно задавать с помощью функции распределения.
Определение: Функцией распределения непрерывной случайной величины Х называется функция F(х), определяющая для каждого значения х 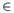 R
R
вероятность того, что случайная величины Х в результате испытания примет значение, меньшее х:
F(x)=P(X<x),где х 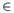 R
R
Функцию распределения иногда называют интегральной функцией распределения.
Свойства функции распределения:
1)1≤ F(x) ≤1
2)У непрерывной случайной величины функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.
3) Вероятность попадания случайной величины Х в один из промежутков (а;b), [а;b), [а;b], равна разности значений функции F(х) в точках а и b,т.е. Р(а<Х<b)= F(b)- F(a)
4)Вероятность того, что непрерывная случайная величина Х примет одно отдельное значение равна 0.
5) F(-∞)=0, F(+∞)=1
Задание непрерывной случайной величины с помощью функции распределения не является единственным. Введем понятие плотности распределения вероятностей (плотность распределения).
Определение: Плотностью распределения вероятностей f(x) непрерывной случайной величины Х называется производная от ее функции распределения, т.е.:
f(x)=F’(x)
Плотность распределения вероятностей иногда называют дифференциальной функцией распределения или дифференциальным законом распределения.
Графикплотности распределения вероятностей f(x) называется кривой распределения вероятностей.
Свойства плотности распределения вероятностей:
1)f(x) ≥0,при х 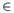 R
R
х
2) F(x)= ∫ f(x)dx
-∞
Геометрически функция распределения равна площади фигуры, ограниченной сверху кривой распределения снизу осью ОХ и лежащей левее точки х (рис.1)
b
3) Р(а<Х<b)= ∫ f(x)dx
a
Геометрически полученная вероятность равна площади криволинейной трапеции, ограниченной сверху кривой распределения, снизу осью ОХ, слева и справа прямыми х=а, х=b (рис. 2)
-∞
4) ∫ f(x) dx=1-условие нормировки
+∞
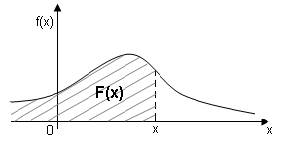
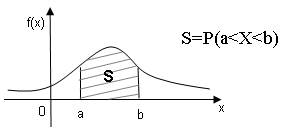
рис.1 рис.2
Задача №1.Случайная величина Х задана плотностью распределения вероятностей:
 0 при х≤2,
0 при х≤2,
f(x)= с(х-2) при 2<х≤6,
0 при х>6.
Найти: а) значение с; б) функцию распределения F(х) и построить ее график; в) Р(3≤х<5)
Решение:
+∞
а) Значение с найдем из условия нормировки: ∫ f(x)dx=1.
Следовательно, -∞
 +∞ 2 6 +∞ 6 6
+∞ 2 6 +∞ 6 6
∫ f(x)dx=∫ 0dx+ ∫ c(х-2)dx +∫ 0dx= c∫ (х-2)dx=с(х2/2-2х) =с(36/2-12-(4/2-4))=8с;
-∞ -∞ 2 6 2 2
8с=1;
с=1/8.
х
б) Известно, что F(x)= ∫ f(x)dx
-∞
Поэтому, х
если х≤2, то F(x)= ∫ 0dx=0;
 -∞ 2 2 х
-∞ 2 2 х
если 2<х≤6, то F(x)= ∫ 0dx+∫ 1/8(х-2)dx=1/8(х2/2-2х) = 1/8(х2/2-2х- (4/2-4))=
-∞ -∞ 2
=1/8(х2/2-2х+2)=1/16(х-2)2;
 2 6 х 6 6
2 6 х 6 6
если х>6, то F(x)= ∫ 0dx+∫ 1/8(х-2)dx+∫ 0dx=1/8∫(х-2)dx=1/8(х2/2-2х) =
-∞ 2 6 2 2
=1/8(36/2-12-(4/2+4))=1/8•8=1.
Таким образом,
 0 при х≤2,
0 при х≤2,
F(х)= (х-2)2/16 при 2<х≤6,
1 при х>6.
График функции F(х) изображен на рис.3
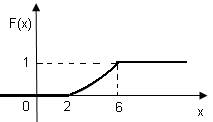
рис.3
в) Р(3≤Х<5)=F(5)-F(3)=(5-2)2/16-(3-2)2/16=9/16-1/16=5/16.
Задача №2.Случайная величина Х задана функцией распределения:
 0 при х≤0,
0 при х≤0,
F(х)= (3• arctg х)/π при 0<х≤√3,
1 при х>√3.
Найти дифференциальную функцию распределения f(х)
Решение: Т.к.f(х)= F’(x), то
 0 при х≤0,
0 при х≤0,
f(х)= (3•(1+х2)) /π при 0<х≤√3,
0 при х>√3.
Дата добавления: 2016-07-18; просмотров: 5225;











