Показательный (экспоненциальный) закон распределения

Определение:Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметромλ>0, если функция плотности распределения вероятностей имеет вид:

0 при х<0,

f(х)= λе^-λх при х≥0.

Функция распределения случайной величины Х, распределенной по показательному закону, задается формулой:

0 при х≤3,

F(х)= 1-e^-λх при х≥0.

Кривая распределения f (х) и график функции распределения F(х) случайной величины Х приведены на рис.5 и рис.6.

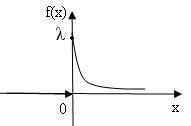рис.5 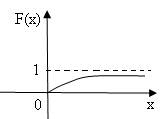рис.6

Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного распределения соответственно равны:

M(X)= 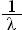, D(X)= 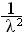, σ (Х)=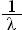

Таким образом, математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.

Вероятность попадания Х в интервал (a;b) вычисляется по формуле:

Р(a<Х<b)= e^-λа- e^-λb

Задача №2.Среднее время безотказной работы прибора равно 100 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:

а) плотность распределения вероятностей;

б) функцию распределения;

в) вероятность того, что время безотказной работы прибора превысит 120 ч.

Решение: По условию математическое распределение M(X)= 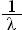=100, откуда λ=1/100=0,01.