Расчет магнитной цепи переменного потока комплексным методом
Машины переменного тока, трансформаторы, в которых ферромагнитные сердечники подвергаются периодическому перемагничиванию, работают в режиме вынужденного синусоидального напряжения на их обмотках. Рассмотрим работу магнитной цепи на примере сердечника трансформатора (рис. 252а). К обмотке трансформатора приложено синусоидальное напряжение 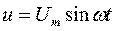 , геометрические размеры магнитопровода и характеристики его материала заданы.
, геометрические размеры магнитопровода и характеристики его материала заданы.
Из уравнения электромагнитной индукции 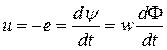 следует:
следует:
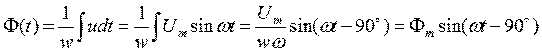

Магнитный поток ф(t) жeстко связан с напряжением u(t), изменяется по синусоидальному закону с отставанием от напряжения на 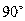 . Таким образом, в схеме замещения магнитной цепи источник энергии представляется источником магнитного потока ф(t), где
. Таким образом, в схеме замещения магнитной цепи источник энергии представляется источником магнитного потока ф(t), где
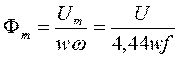 [Вб],
[Вб], 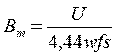 [Тл].
[Тл].
Заменим синусоидальные функции их комплексными изображениями:
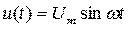 Þ
Þ 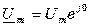 ;
;
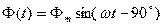 Þ
Þ 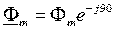 .
.
Вследствие нелинейной зависимости В=f(Н) намагничивающий ток в обмотке будет несинусоидальным. Заменим несинусоидальную функцию тока i(t) эквивалентной синусоидальной:
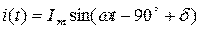 Þ
Þ 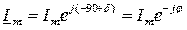 .
.
Вследствие потерь в сердечнике на премагничивание магнитный поток 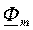 отстает по фазе на некоторый угол δ от вектора тока
отстает по фазе на некоторый угол δ от вектора тока 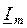 . Угол отставания δ получил в технике название угла потерь. Очевидно из векторной диаграммы (рис. 55), что δ = 90˚-φ или φ = 90˚- δ.
. Угол отставания δ получил в технике название угла потерь. Очевидно из векторной диаграммы (рис. 55), что δ = 90˚-φ или φ = 90˚- δ.
После замены всех функций времени их комплексными изображениями дальнейшее исследование процессов в магнитной цепи можно проводить в комплексной форме.
Комплексное магнитное сопротивление сердечника:
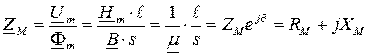 ,
,
где 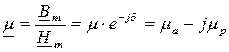 - комплексная магнитная проницаемость.
- комплексная магнитная проницаемость.
Из справочной литературы находим для расчетной амплитуды индукции 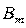 соответствующие значения мощности удельных потерь
соответствующие значения мощности удельных потерь 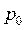 и удельной намагничивающей мощности
и удельной намагничивающей мощности 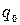 . Суммарные значения этих мощностей для всего сердечника составят:
. Суммарные значения этих мощностей для всего сердечника составят:
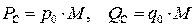 , где M- масса сердечника [кг].
, где M- масса сердечника [кг].
Активное и реактивное магнитные сопротивления сердечника выражаются через суммарные мощности:
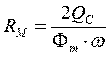 ,
, 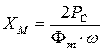 .
.
Магнитное сопротивление воздушного зазора носит чисто активный характер и определяется через его геометрические размеры:
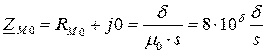 .
.
Эквивалентное магнитное сопротивление всей цепи:
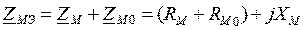
МДС обмотки и магнитный поток в сердечнике связаны между собой законом Ома:
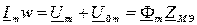 , откуда следует:
, откуда следует:
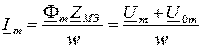 .
.
Векторная диаграмма для всех величин показана на рис. 253:

Дата добавления: 2020-07-18; просмотров: 513;











