Определение коэффициентов четырехполюсника

Коэффициенты четырехполюсника могут быть определены расчетным или экспери­ментальным путем. Если известна внутренняя структура (схема) четырехполюсника и пара­метры отдельных элементов, то коэффициенты четы­рехполюсника определяются расчетным путем по одному из двух методов.

Сущность первого метода состоит в том, что сложная схема четырехпо­люсника путем последовательных преобразований сворачивается к простейшей Т- или П-образной схеме. Коэффициенты четырехполюсника определяются по соответствующим формулам, получен­ным ранее для этих схем.

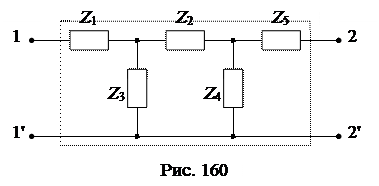Пусть требуется определить коэффициенты четырехполюсника, схема ко­торого при­ведена на рис. 160.

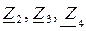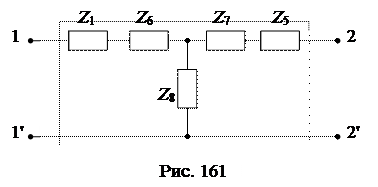
Выполняется первое преобразование: треугольник преобразу­ется в эквива­лентную звезду 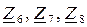(рис. 161):

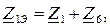
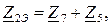
Затем выполняются последовательные преобразования 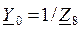, после чего схема получает стандартный Т-образный вид (рис. 162):

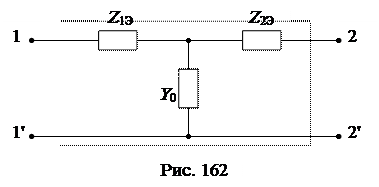Коэффициенты четырехполюсника находятся по формулам для Т-схемы:

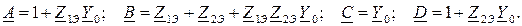
Сущность второго метода заключается в том, что коэффициенты четы­рехполюсника определяются через его входные сопротивления со стороны входных ( Z_1X и Z_1K) и выход­ных (Z_2X и Z_2K) выводов в режимах холостого хода и короткого замыкания на противо­полож­ной стороне. Значения этих сопротив­лений рассчитываются аналитически методом свертки схемы четырехполюс­ника в соответствующем режиме (х.х. или к.з.) относительно его выво­дов.

При питании четырехполюсника со стороны первичных выводов приме­няются урав­нения формы А:

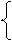U₂ = D·U₁ + B·I₁ ,

I₂ = C·U₁ + A·I₁.

В режиме холостого хода на вторичной стороне I_2X = 0, а в режиме корот­кого замыка­ния U_2K = 0. Из уравнений следует:

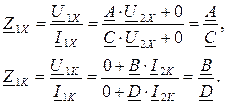
При питании четырехполюсника со стороны вторичных выводов приме­няются урав­нения формы В:

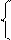U₂ = D·U₁ + B·I₁,

I₂ = C·U₁ + A·I₁.

В режиме холостого хода на первичной стороне I_1X = 0, а в режиме корот­кого замыка­ния - U_1K = 0. Из уравнений следует:

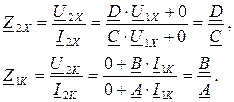
Совместное решение полученных уравнений позволяет установить связь между вход­ными сопротивлениями четырехполюсника в режиме холостого хода и короткого замыкания, но не дает возможности определить его коэффи­циенты:

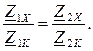
Для определения коэффициентов четырехполюсника берут любые три из четырех уравнений для входных сопротивлений и дополняют их уравнением связи между коэффици­ентами A×D -B×C = 1, после чего решают полученную систему из четырех уравнений. В каче­стве примера возьмем уравнения для Z_1X, Z_2X и Z_2K, тогда получим:

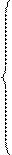
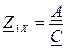, откуда 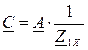(1)

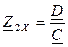, откуда 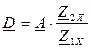(2)

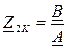, откуда 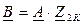(3)

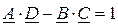(4)

Из уравнений (1), (2) и (3) делаем подстановку в уравнение (4), получим:

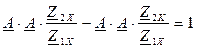, откуда следует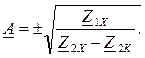

Остальные коэффициенты (B, C, D) получим путем подстановки найден­ного значения А в уравнения (1), (2) и (3).

При извлечении квадратного корня получаются два значения коэффици­ента А и, соот­ветственно, всех остальных коэффициентов, отличающиеся зна­ком (+ или -) или аргументом в 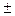180^о, например ,

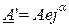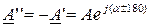
Двойственность решения объясняется тем фактом, что входные сопротив­ления любой цепи, в том числе четырехполюсника, не зависят от полярности выводов. С другой стороны, изменения полярности двух выводов четырехпо­люсника (1 Û 1' или 2 Û 2') приводит к из­менению знаков перед всеми его ко­эффициентами. Таким образом, для утверждения знаков перед коэффициен­тами необходимы дополнительные исследования.

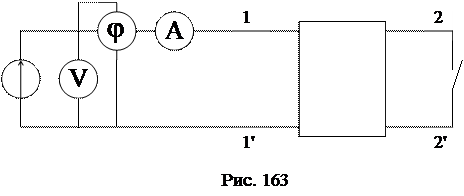
Входные комплексные сопротивления четырехполюсника могут быть из­мерены экс­периментально по схеме рис. 163:

П

Комплексное входное сопротивление цепи находится по формуле:

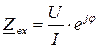, где U, I, j -показания приборов в исследуемой цепи.