Способы соединения четырехполюсников

Сложная цепь или схема может содержать несколько четырехполюсников, соединен­ных между собой тем или иным образом. При расчете таких схем от­дельные группы четы­рехполюсников можно заменить эквивалентными одиноч­ными четырехполюсниками и, та­ким образом, упростить схему цепи и, соответ­ственно, решение задачи.

Различают 5 способов соединения четырехполюсников между собой: а ) каскадное, б) последовательное, в) параллельное, г) последовательно-парал­лельное, д) параллельно-после­довательное.

На рис. 164 показано каскадное соединение двух четырехполюсников П' и П'':

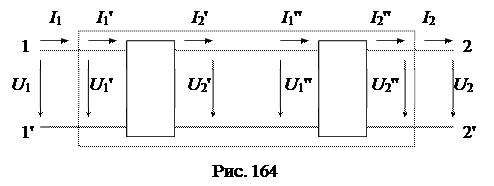Для каскадного соединения, как видно из схемы удовлетворяются сле­дующие равен­ства (в матричной форме):

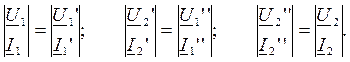
Используя уравнения четырехполюсника формы А, получим:

.

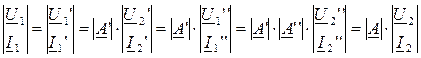Следовательно, матрица коэффициентов эквивалентного четырехполос­ника равен произведению матриц каскадно включенных четырехполосников:

.

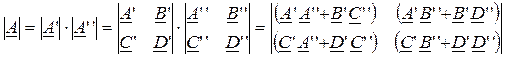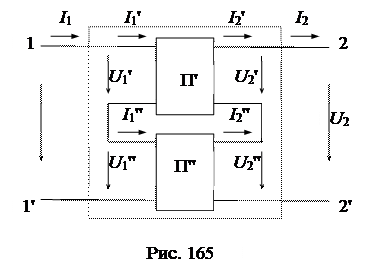При последовательном соединении двух четырехполюсников включаются последова­тельно их входы и последовательно их выходы (рис. 165):

Для последовательного соединения, как следует из схемы (рис. 165), удов­летворяются следующие равенства:

.

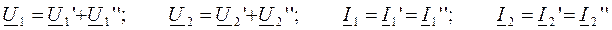Используя уравнения четырехполюсника формы Z, получим:

.

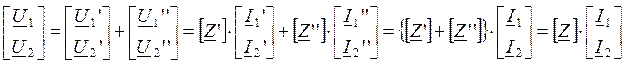Следовательно, матрица коэффициентов 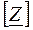эквивалентного четырехпо­люсника равна сумме матриц последовательно включенных четырехполюсни­ков: .

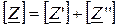При параллельном соединении двух четырехполюсников включаются па­раллельно их входы и параллельно их выходы (рис. 166):

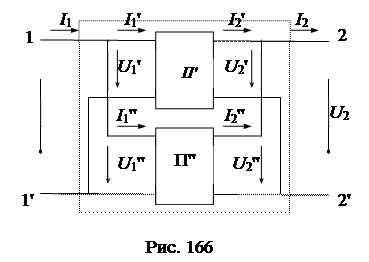Для параллельного соединения, как следует из схемы (рис. 166), удовлетво­ряют сле­дующие равенства:

; ; ; .

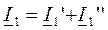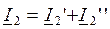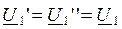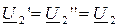Используя уравнения четырехполюсника формулы Y, получим:

.

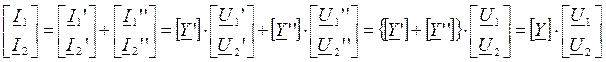Следовательно, матрица коэффициентов [Y] эквивалентного четырехпо­люсника П’ и П’’ их входы включаются последовательно, а выходы – парал­лельно. При свертке схемы ис­пользуются уравнения формы Н:

,

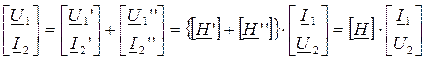где 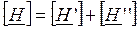- матрица коэффициентов [H] эквивалентного че­тырехполюс­ника.

При параллельно-последовательном соединении двух четырехполюсни­ков 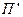и и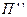х входы включаются параллельно, а выходы – последовательно. При свертке схемы исполь­зуются уравнения формы G:

,

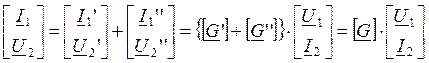где 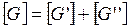– матрица коэффициентов [G] эквивалентного четырех­полюс­ника.

5. Характеристические параметры симметричного четырехполюсника

Для симметричного четырехполюсника коэффициент 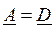и система уравнений формы А имеет вид:

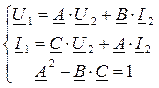
Характеристическим сопротивлением четырехполюсника 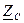называется такое сопро­тивление нагрузки 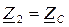, при котором входное сопротивление четырехполюсника со сто­роны первичных выводов также равно сопротивлению нагрузки:

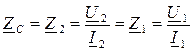
Установим связь между характеристическим сопротивлением 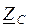и ко­эффициентами четырeхполюсника А, В, С. Для этой цели преобразуем уравне­ния четырехполюсника:

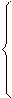
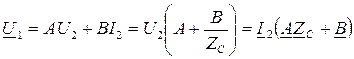(1)

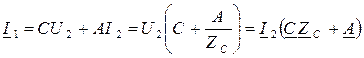(2)

Разделим уравнение (1) на уравнение (2):

,

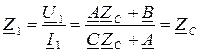откуда получаем 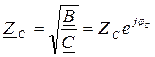, где ;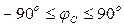

из (1) Þ ;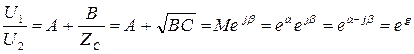

из (2) Þ ,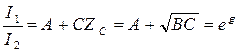

где g = α + jβ = ln( 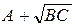) – постоянная (коэффициент) передачи четы­рехполюс­ника.

Вещественная часть коэффициента передачи a показывает, как изменя­ется модуль на­пряжения (тока) при переходе через четырехполюсник, поэтому называется коэффициентом затухания:

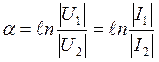[Hп] или [Непер] – основная единица измерения затухания.

Затухание в 1Нп соответствует уменьшению модуля величины в е = 2,72 раза. На практике для измерения затухания сигналов применяется другая, более удобная для практики единица, а именно: 1 децибелл [дБ], которая определя­ется согласно уравнению:

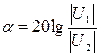[дБ] ; 1 дБ = 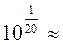1,122 раза.

Соотношение между единицами затухания: 1Нп = 8,086 дБ ; 1дБ = 0,115Нп.

Мнимая часть коэффициента передачи показывает, как изменяется фаза напряжения (тока) при переходе через четырехполюсник, поэтому называется коэффициентом фазы:

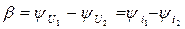[рад]

Характеристическое сопротивление 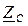и коэффициент передачи 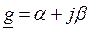называ­ются характеристическими параметрами четырехполюсника.

Выразим коэффициенты четырехполюсника через его характеристические параметры 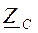и .

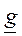Преобразуем уравнение связи между коэффициентами:

.

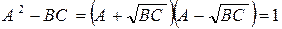Так как 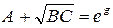, то следовательно .

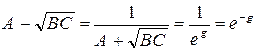Решаем совместно полученные уравнения:

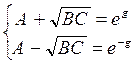
Откуда следует, что , .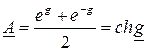

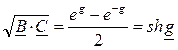Учитывая, что 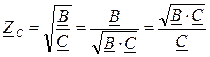, получим для коэффициентов:

, .

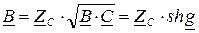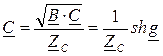С учетом этих выражений основные уравнения формы А получат оконча­тельный вид:

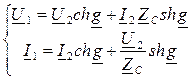
Данная форма уравнений четырехполюсника используется в теории цеп­ных схем и в теории электрических фильтров.

Основные понятия и определения электрических фильтров

Электрическим фильтром называется четырехполюсник, предназначен­ный для выде­ления (пропускания) сигналов определенной полосы частот. В за­висимости от пропускае­мого спектра частот фильтры подразделяют на 4 основ­ных вида:

1) фильтры низких частот (ФНЧ), пропускающие сигналы в диапазоне частот от w₁=0 до w₂;

2) фильтры высоких частот (ФВЧ), пропускающие сигналы в диапазоне частот от w₁ до ;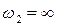

3) полосовые фильтры (ПФ), пропускающие сигналы в диапазоне частот от w₁ до w₂;

4) заграждающие или режекторные фильтры (ЗФ), пропускающие сиг­налы в диапазоне частот от 0 до w₁ и в диапазоне частот от w₂ до 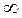и не про­пускающие сигналы в диапазоне частот от w₁ до w₂.

Коэффициентом передачи напряжения фильтра называется отношение комплексных выходного напряжения ко входному:

,

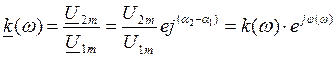где 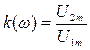показывает, как изменяется с частотой амплитуда выходного напряжения, и называется амплитудно-частотной характеристикой (АЧХ) фильтра; j(w)=(a₂-a₁) показы­вает, как изменяется с частотой фаза выходного напряжения, и называется фазо-частотной характеристикой (ФЧХ) фильтра.

Диапазон частот, в котором фильтр пропускает к приемнику сигналы практиче­ски без изменения, называется полосой пропускания или зоной прозрачности фильтра. В полосе пропускания для идеального фильтра должны удовлетво­ряться два условия: 1) 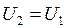, при этом 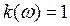; 2) j(w)=-tw, при этом все гармоники сигнала будут иметь одинаковое время запаздывания 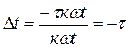. При выполнении этих условий сигнал на выходе фильтра не изменится.

Электрические фильтры можно классифицировать:

1) по типу элементов, из которых они состоят, на а)реактивные, состоя­щие только из реактивных элементов L и C; б)безиндукционные, состоящие из элементов R и C; и др.;

2) по способу соединения элементов между собой на Т-, П- и Г-образные;

3) по виду частотных характеристик на типа “k” и типа “m”.

Электрические фильтры широко применяются в радиотехнике, в технике связи. В электроэнергетике фильтры применяются для сглаживания пульсаций выпрямленного на­пряжения.