Уравнения четырехполюсника
Четырехполюсником называется часть электрической цепи или схемы, содержащая два входных вывода (полюса) для подключения источника энергии и два выходных вывода для подключения нагрузки. К четырехполюсникам можно отнести различные по назначению технические устройства: двухпроводную линию, двухобмоточный трансформатор, фильтры частот, усилители сигналов и др.
Теория четырехполюсников устанавливает связь между режимными параметрами на входе (U1, I1) и режимными параметрами на его выходе (U2, I2), при этом процессы, происходящие внутри четырехполюсника, не рассматриваются. Таким образом, единая теория четырехполюсника позволяет анализировать различные по структуре и назначению электрические цепи, которые могут быть отнесены к классу четырехполюсников.
Если четырехполюсник не содержит внутри себя источников энергии, то он называется пассивным (обозначается буквой П), если внутри четырехполюсника имеются источники, то он называется активным (обозначается буквой А).
В настоящей главе анализируются пассивные линейные четырехполюсники. На электрических схемах четырехполюсники условно обозначаются прямоугольником с двумя парами выводов: 1 и 1' - входные выводы, 2 и 2' - выходные выводы (рис. 1). Соответственно напряжение и ток на входе индексируются цифрой 1 (U1, I1) , а на выходе - цифрой 2 (U2, I2).
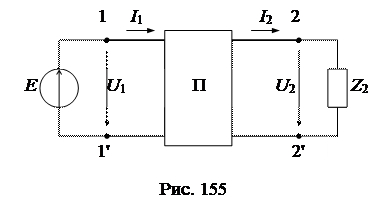 |
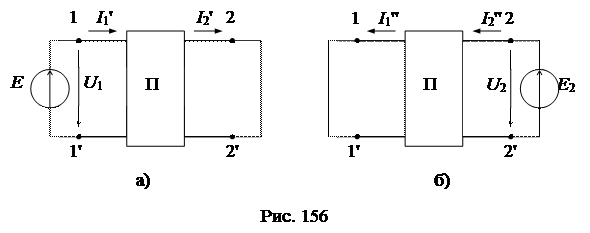
Установим связь между параметрами режима входа (U1, I1) и выхода (U2, I2). Для этой цели согласно теореме о компенсации заменим нагрузку Z2 источником ЭДС Е2 = U2 = I2Z2 и найдем токи по методу наложения от каждого источника в отдельности (рис. 156а, б):
 |
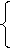
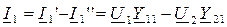
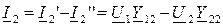 ,
,
где Y11, Y22 – входные проводимости входа и выхода, Y12 = Y21 – взаимная проводимость между входом и выходом.
Выразим из полученных уравнений режимные параметры на входе:
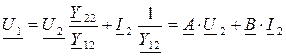
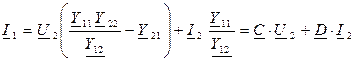 ,
,
где 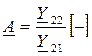 ;
; 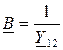 [Ом];
[Ом]; 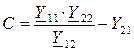 [См];
[См]; 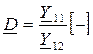 – комплексные коэффициенты четырехполюсника.
– комплексные коэффициенты четырехполюсника.
С учетом принятых обозначений система основных уравнений четырехполюсника получит вид:
|
|
Уравнения четырехполюсника часто записывают в матричной форме:
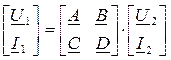 или
или 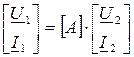 ,
,
где 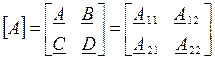 - матрица коэффициентов формы А.
- матрица коэффициентов формы А.
Выразим соотношение между коэффициентами четырехполюсника:
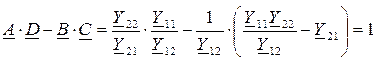
A·D - B·C=1 – уравнение связи между коэффициентами. Уравнение связи показывает, что независимыми являются только три из четырех коэффициентов четырехполюсника.
Поменяем местами в схеме рис. 155 источник и приемник энергии. В новой схеме рис. 157 направления токов изменятся на противоположные.
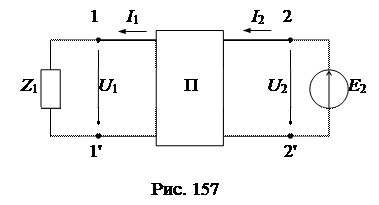 |
Уравнения четырехполюсника с учетом изменения направлений токов примут вид:
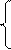
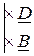
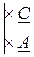
Преобразуем полученную систему уравнений следующим образом. Умножим члены уравнения (1) на D, члены уравнения (2) на В и вычтем почленно из 1-го уравнения 2-ое. В результате получим:
D·U1 + B·I1 = (A·D - B·C)·U2 + (B·D - B·D)·I2 = U2.
Умножим члены уравнения (1) на С, члены уравнения (2) на А и вычтем из 1-го уравнения 2-ое. В результате получим:
C·U1 + A·I1 = (A·C - A·C)·U2 + (A·D - B·C)·I2 = I2
Новая система уравнений четырехполюсника получила название формы В:
|
|
Четырехполюсник называется симметричным, если перемена местами входных и выходных выводов не влияет на режим остальной цепи, частью которой является четырёхполюсник. Для симметричного четырёхполюсника А=D и A2 - B·C=1.
Кроме названных форм уравнений четырехполюсника А и В применяются на практике еще четыре формы, а именно формы Z, Y, H и G. Структура этих уравнений приведена ниже:
|
| ||||||||
|
| ||||||||
|
| ||||||||
|
|
Для уравнений формы Z, Y, H и G принята следующая ориентация токов и напряжений относительно выводов четырехполюсника (рис.158).
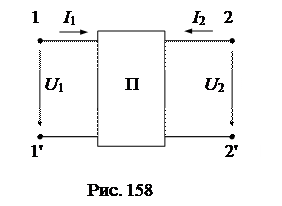 |
Соотношения между коэффициентами четырехполюсника различных форм приводятся в справочной литературе, однако их нетрудно получить, выполнив преобразование одной формы уравнений в другую. Например, пусть заданы коэффициенты формы А (А, В, С, D) и требуется определить коэффициенты формы Z(Z11, Z12, Z21, Z22). Для этого в уравнениях формы A изменим знак тока I2 и решим их относительно переменных U1 и U2:
U1 = A·U2 - B·I2 (1)
I1 = C·U2 - D·I2 (2)
Из (2) следует: 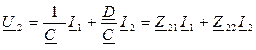 .
.
Из (1) следует: 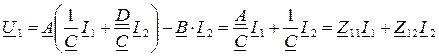 .
.
Сравнивая полученные выражения с уравнениями четырехполюсника формы Z, находим соотношения между коэффициентами двух форм:
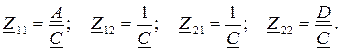
Дата добавления: 2020-07-18; просмотров: 596;











