Высшие гармоники в трехфазных цепях

В симметричном трехфазном режиме токи и напряжения в фазах сдви­нуты взаимно во времени на Dt = T/3 в порядке следования фаз А ® В ® С ® А, что в градусной мере со­ставляет : для 1 гармоники Dwt = 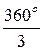= 120°, для 2 гармоники D2wt = 2× 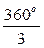= 240= -120°, для 3 гармоники D3wt = 3× 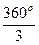= 360° = 0, и т. д.

Из этого следует, что в симметричной трехфазной системе гармоники с порядко­вым номером к = 3n-2 (n = 1, 2, 3…), т.е. 1-я, 4-я, 7-я и т.д., имеют пря­мой порядок следова­ния фаз А ® В ® С ® А и, следовательно, образуют сим­метричные системы прямой после­дова­тель­ности. Гармоники с порядковым но­мером к = 3n+1 (2-я, 5-я, 8-я и т.д.) имеют обрат­ный по­рядок следования фаз А ® С ® В ® А и, следовательно, образуют симметричные сис­темы обратной последовательности. Гармоники с порядковым номером к=3n (3-я, 6-я, 9-я и т.д.) имеют нулевой порядок следования фаз, т.е. совпадают, и, следовательно, образуют симмет­ричные системы нулевой последовательности.

Пусть обмотки трехфазного генератора соединены по схеме звезды с выводом ну­левой точки, а его фазные напряжения (ЭДС) содержат все возмож­ные гармоники (рис. 125).

UA     UB UC

B функциях фазных напряжений будут содержаться все гармоники с соот­ветствую­щими их номеру сдвигами фаз:

u_A(t) = U_1msinwt +U_2msin2wt + U_3msin3wt + …

u_B(t) = U_1msin(wt - 120°) +U_2msin(2wt + 120°) + U_3msin3wt + …

u_C(t) = U_1msin(wt +120°) +U_2msin(2wt - 120°) + U_3msin3wt + …

Векторные диаграммы напряжений для 1-й, 2-й и 3-й гармоник пока­заны на рис. 126а, б, в.

Линейные напряжения равны разности соответствующих двух фазных на­пряжений, например u_AB = u_A - u_B. Как следует из векторных диаграмм рис. 9 амплитуды линейных на­пряжений для гармоник прямой и обратной последова­тельностей в 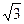раз больше их фазных значений, а гармоники нулевой последо­вательности (кратные трем) в линейных напряжениях вообще отсутствуют (равны нулю):

u_AB(t) =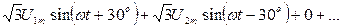

u_BC(t) =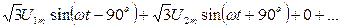

u_CA(t) =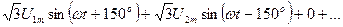

Действующие значения фазного и линейного напряжения :

;

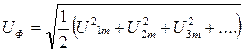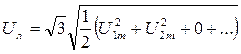
Сравнение полученных уравнений показывает, что при наличии в фазных напряже­ниях генератора гармоник нулевой последовательности (кратных трем) стандартное соотно­шение 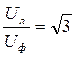не соблюдается, а именно 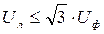. Из совместного решения этих урав­нений получим : 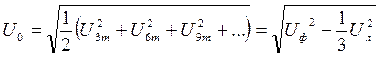- действующее значение всех гармоник нулевой последовательности. В реальных трехфазных цепях четные гармо­ники, как правило, отсутствуют вообще, а амплитуда 9-й гармоники не­значительна, поэтому можно приближенно считать, что U₀» U₃ , и U_3m» 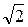U₀ - амплитуда 3-й гармоники.

Если обмотки трехфазного генератора соединить по схеме треуголь­ника, то гармо­ники прямой и обратной последовательностей в контуре тре­угольника складываясь, в сумме дают нуль, а гармоники нулевой последова­тельности складываются арифметически, и в кон­туре треугольника будет дейст­вовать суммарная ЭДС, равная 3U₀. Даже при незначительных амплитудах гар­моник нулевой последовательности в фазных ЭДС, вызываемые ими в кон­туре треугольника токи могут оказаться значительными по величине, так как внут­реннее сопротивление обмоток очень мало. Это привело бы к до­полнительным потерям энергии в генераторе и снижению его КПД. По этой причине обмотки трехфазных генераторов запрещается соединять по схеме треугольника.

Расчет трехфазной цепи при несинусоидальном напряжении генератора произво­дится так же, как и любой сложной цепи, а именно, по методу наложе­ния в три этапа. На 1-ом этапе выполняется разложение несинусоидального фазного напряжения в гармонический ряд Фурье. На 2-ом этапе выполняется расчет схемы для каждой гармоники в отдельности, при этом учитывается зави­симость порядка следования фаз от номера гармоники. Например, гар­моники токов нулевой последовательности могут замкнуться только через нулевой про­вод, поэтому при отсутствии нулевого провода гармоники кратные трем в фаз­ных и линейных токах равны нулю.

На заключительном этапе расчета определяются действующие значе­ния токов, на­пряжений, активные мощности.

В случае симметричной трехфазной нагрузки расчет токов и напряже­ний для каж­дой гармоники можно выполнять только в одной фазе А, а соответ­ствующие токи и напряже­ния в других фазах определять через поворотные множители “ а ”, “ а² ” с учетом порядка следования фаз.

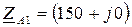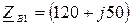Пример. Задана схема цепи (рис. 127) и комплексные сопротивления фаз на основной частоте ( Ом, Ом, 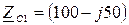Ом. Фазные напряжения генератора несинусоидальны, гармо­нический состав задан :

u_A = 200sinwt + 50sin3wt + 20sin5wt

Требуется определить : 1) действующие значения фазных и линейных на­пряжений генератора, 2) действующие значения линейных (фазных) токов при­емника и тока в нулевом проводе, 3) активные мощности генератора и прием­ника.

Расчет схемы для 1-й гармоники (прямая последовательность):

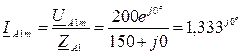
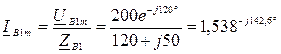
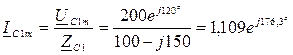
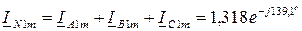
Расчет схемы для 3-й гармоники (нулевая последовательность) :

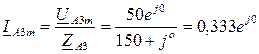
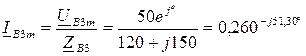
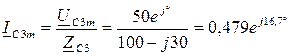
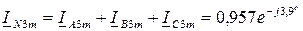
Расчет схемы для 5-й гармоники (обратная последовательность) :

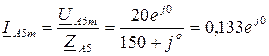
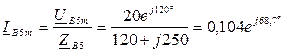
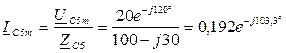
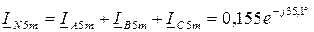
Синтез решения.

Действующие значения фазного и линейного напряжений :

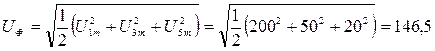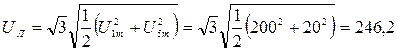В

В

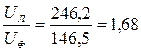B, что меньше .

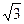Действующие значения токов :

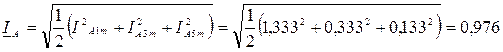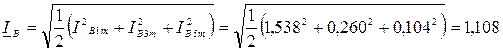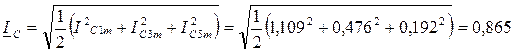A

A

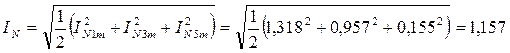A

A

Так как при наличии нулевого провода отдельные фазы приемника рабо­тают незави­симо друг от друга, то активные мощности отдельных фаз прием­ника равны активным мощ­ностям одноименных фаз генератора.

P_A = I²_A×R_A = 0.976²×150 = 142.9 Вт

P_B = I²_B×R_B = 1.108²×120 = 147.3 Вт

P_C = I²_C×R_C = 0.865²×100 = 74.8 Вт

P = P_A + P_B + P_C = 365 Вт

Т9. Переходные процессы в электрических цепях