Виды симметрии периодических функций

Различают следующие виды симметрии периодических несинусоидаль­ных функций.

1) Нечетная симметрия: функция симметрична относительно начала ко­ординат и удовлетворяет условию 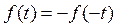(рис. 119).

Функции, обладающие нечетной симметрией, получили название нечет­ных. В раз­ло­жении таких функций содержатся только синусные составляющие отдельных гармоник B_k и отсутствуют постоянная составляющая A₀ и косинус­ные составляющие отдельных гармо­ник С_k:

.

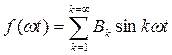При определении коэффициентов ряда Фурье нечетной функции интегри­рование в формуле достаточно выполнить за половину периода T/2:

.

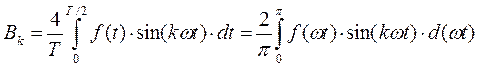2) Четная симметрия: функция симметрична относительно оси ординат и удовлетво­ряет условию 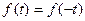(рис. 3).

Функции, обладающие четной симметрией, получили название четных. В разложе­нии таких функций содержатся только постоянная составляющая А₀ и косинусные состав­ляющие отдельных гармоник C_k и отсутствуют синусные со­ставляющие отдельных гармоник В_к:

.

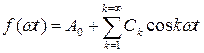При определении коэффициентов ряда Фурье четной функции интегри­рование в формулах достаточно выполнить за половину периода:

,

.

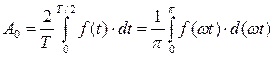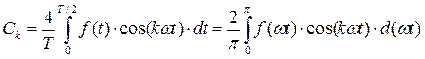3) Косая симметрия: функция симметрична относительно оси абсцисс при смещении ее положительной части [f(t)>0] или отрицательной части [f(t)<0] на отрезок времени 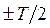и удовлетворяет условию 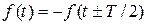(рис. 121):

Функции, обладающие косой симметрией, получили название кососим­метричных. В разложении таких функций содержатся только нечетные гармо­ники (синусные и косинусные составляющие):

.

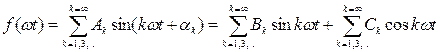Докажем это утверждение методом от обратного. Предположим, что ко­сосиммет­рич­ная функция содержит в разложении все члены ряда Фурье:

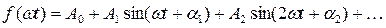
Добавим к аргументу функции T/2:

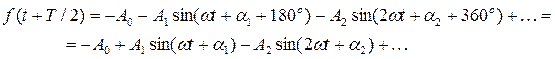
Равенство 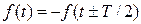выполняется при условии A₀=0, A₂=0, A₄=0,…, что тре­бо­валось доказать.

Коэффициенты ряда Фурье кососимметричной функции определяются по общим пра­вилам.

Функция f(t) может обладать одновременно двумя видами симметрии, на­пример, не­четной и косой или четной и косой, но не может быть одновременно нечетной и четной. При разложении конкретной функции в ряд Фурье начало отсчета следует выбрать так, чтобы получить желаемый вид симметрии функ­ции.

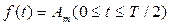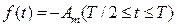Пример. Требуется разложить в ряд Фурье периодическую прямоуголь­ную функ­цию и (рис. 122).

При выбранном начале отсчета (точка 0) функция будет обладать одно­временно двумя видами симметрии (нечетной и косой) и ее гармонический со­став будет иметь вид:

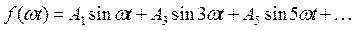
Коэффициенты ряда Фурье определяются по формуле для нечетной функ­ции:

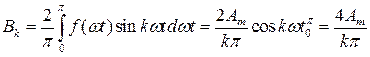
Тогда ряд Фурье исследуемой функции получит вид:

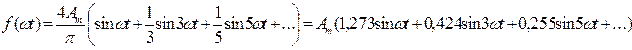
4. Действующие значения несинусоидальных токов и напряжений

Как известно, в электроэнергетике переменные токи и напряжения харак­теризуются их действующими значениями. Математически действующее значе­ние любого периодически изменяющегося тока (напряжения) определяется как среднеквадратичное значение функции за период:

;

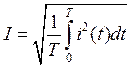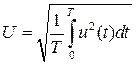
Пусть функция тока содержит в своем составе все компоненты ряда Фу­рье:

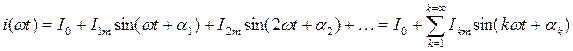
Определим действующее значение этой функции:

=

=

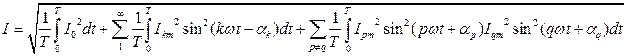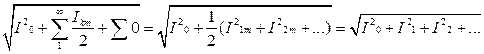
При интегрировании учтено, что произведение двух синусоидальных функций вре­мени с различными частотам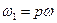и и 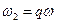дает сумму двух новых синусоидальных функций с частотам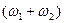и и 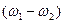, определенный интеграл от которых в пределах целого числа периодов равен нулю.

Итак получено, что действующее значение несинусоидального тока (на­пряжения) равно квадратному корню из действующих значений отдельных гар­моник:

,

.

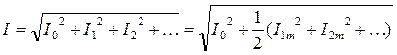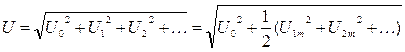Примерынекоторых функций и их действующих значений приведены ниже:

1. ;

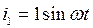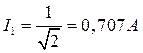
2. ;

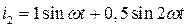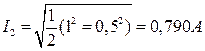
3. ;

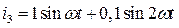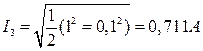
Вывод: при коэффициенте высшей гармоники менее 0,1 ( 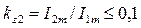) их доля в действующем значении функции составляет менее 1% ( 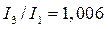), и, следовательно, при определении действующего значения функции с по­грешностью 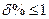эти гармоники могут не учиты­ваться.