Расчет электрических цепей несинусоидального тока
Расчет электрических цепей, содержащих источники энергии [источники ЭДС e(t)и источники тока j(t)] с несинусоидальной формой кривой, выполняется по методу положения. Процедуру расчета можно условно разделить на три этапа.
1)Гармонический анализ.
На этом этапе выполняется разложение несинусоидальных функций источников ЭДС e(t)и источников тока j(t)в гармонический ряд Фурье:
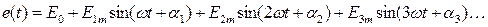
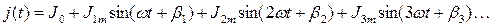
Для проведения анализа структуры функций e(t) и j(t)количество гармоник в их разложении определяютзначительно больше, чем необходимо для расчета схемы.
2)Аналитический расчет.
Производится аналитический расчет схемы последовательно для каждой гармоники в отдельности. Для постоянной составляющей расчет производится как для резистивной цепи постоянного тока, при этом участки с катушками L закорачиваются, а ветви с конденсаторами C размыкается. Расчет схемы для отдельных гармоник производится как для цепи синусоидального тока, т.е. в комплексной форме, при этом определяются не действующие значения, а комплексные амплитуды токов и напряжений ( 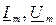 ). Расчет для каждой гармоники выполняется по одному и тому же алгоритму, при этом учитывается зависимость реактивных сопротивлений элементов от частоты и, следовательно, от номера гармоники:
). Расчет для каждой гармоники выполняется по одному и тому же алгоритму, при этом учитывается зависимость реактивных сопротивлений элементов от частоты и, следовательно, от номера гармоники: 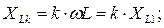
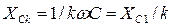 . Выбор расчетного метода определяется структурой расчетной схемы.
. Выбор расчетного метода определяется структурой расчетной схемы.
Количество гармоник, для которых выполняется расчет схемы, устанавливается исходя из конкретных условий задачи. Например, если определяются только действующие значения токов и напряжений (I, U), то достаточно учитывать только те гармоники, для которых коэффициент 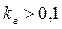 , при этом относительная погрешность расчета в итоге не превысит 1% . Однако в тех случаях, когда требуется проводить исследование форм кривых функций u(t) и i(t), то необходимо учитывать также гармоники более высокого порядка с меньшим коэффициентом гармоник
, при этом относительная погрешность расчета в итоге не превысит 1% . Однако в тех случаях, когда требуется проводить исследование форм кривых функций u(t) и i(t), то необходимо учитывать также гармоники более высокого порядка с меньшим коэффициентом гармоник 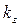 .
.
3.Синтез решения.
На заключительной стадии расчета определяются искомые величины согласно условию задачи.
Мгновенные значения токов и напряжений i(t)и u(t) определяются в соответствии с принципом наложения как алгебраической суммы мгновенных значений отдельных составляющих, например:
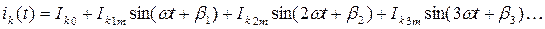
При необходимости исследования формы кривых функций i(t) и u(t) по полученным уравнениям строится их графические диаграммы.
Действующие значения токов и напряжений (I, U) находятся как среднеквадратичные значения этих функций по полученным ранее формулам, например:
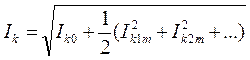
Активные мощности отдельных элементов определяется как суммы активных мощностей этих элементов для отдельных гармоник, например:
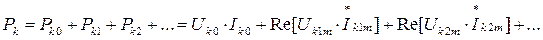
Активную мощность отдельных приемников можно определять также по формуле Джоуля: 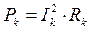 , где
, где 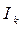 -действующее значение тока этого приемника.
-действующее значение тока этого приемника.
Определяются коэффициенты исследуемых несинусоидальных функций: ku - коэффициент искажения, kф - коэффициент формы, kг - коэффициенты отдельных гармоник и т. д.
Пример. На входе схемы (рис. 123а) с заданными параметрами элементов (R1=30 Ом, R2=20 Ом, L=100 мГн, С=22 мкФ) действует источник несинусоидальной ЭДС (рис. 123б) с частотой f=50 Гц. Требуется определить 1) действующие значения ЭДС Е и токов I, I1, I2; 2) коэффициенты искажения функций ЭДС e(t)и токов i(t), i1(t), i2(t); 3) баланс активных мощностей 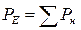 .
.

1-ый этап. Разложение заданной графически функции ЭДС е(t) (рис. 123б) в гармонический ряд Фурье производится с помощью ЭВМ по программе GAR, в результате получим:
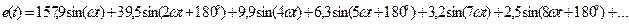
Примечание: гармоники, кратные трем, в разложении данной функции отсутствуют.
2-ой этап. Производится расчет схемы для каждой гармоники в отдельности в комплексной форме по одному и тому же алгоритму:
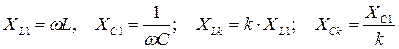 ;
; 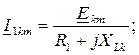
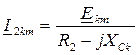 ;
; 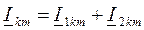 , где k - номер гармоники.
, где k - номер гармоники.
Результаты расчета сведены в общую таблицу. Расчет останавливаем на 5-ой гармонике, так как амплитуды более высоких гармоник в функции e(t) незначительны и их учет уже не повлияет на конечные результаты расчета.
| k | Ekm | Ikm | I1km | I2km |
| 157,9 ej0 | 3,081 e-j30,4 | 3,634 e-j46,3 | 1,080 ej82,1 | |
| 39,5 ej180 | 0,385 ej180 | 0,576 ej115,5 | 0,526 e-j105,4 | |
| 9,9 ej0 | 0,190 ej45,2 | 0,077 e-j76,54 | 0,240 ej61,1 | |
| 6,3 ej180 | 0,154 e-j135,1 | 0,039 ej100,8 | 0,179 e-j124,6 |
3-ый этап. Определяются интегральные параметры искомых функций. Действующие значения функций:
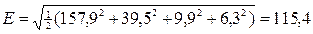 В; I=2,20 A; I1=2,60 A; I3=0,88 A.
В; I=2,20 A; I1=2,60 A; I3=0,88 A.
Коэффициенты искажения формы кривых для функций e(t), i(t), i1(t), i2(t):
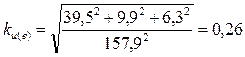 ;
; 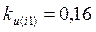 ;
; 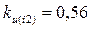 .
.
Активная мощность источника энергии:
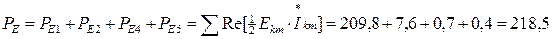 Вт.
Вт.
Активная мощность приемников энергии :
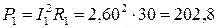 Вт;
Вт; 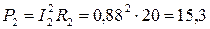 Вт.
Вт.
Баланс мощностей: 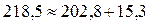
Анализ результатов решения и выводы:
1. Для определения действующих значений величин и активных мощностей можно было бы пренебречь 4-ой и 5-ой гармониками, однако для определения коэффициентов искажения формы кривых учет названных гармоник необходим.
2. Величина и характер входного сопротивления схемы зависит от номера гармоники: для 1-ой гармоники ( 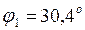 ) – входное сопротивление носит активно-индуктивный характер; для 2-ой гармоники (
) – входное сопротивление носит активно-индуктивный характер; для 2-ой гармоники ( 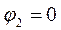 )– входное сопротивление носит чисто активный характер, т.е. на частоте 2-ой гармоники имеет место резонанс токов; для 4-ой гармоники (
)– входное сопротивление носит чисто активный характер, т.е. на частоте 2-ой гармоники имеет место резонанс токов; для 4-ой гармоники ( 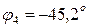 )– входное сопротивление носит активно-емкостный характер.
)– входное сопротивление носит активно-емкостный характер.
3. Форма кривой функции тока i1(t)в ветви с катушкой искажена меньше, чем форма кривой источника ЭДС e(t) ( 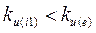 ) , а форма кривой тока i2(t)в ветви с конденсатором, наоборот, искажена больше (
) , а форма кривой тока i2(t)в ветви с конденсатором, наоборот, искажена больше ( 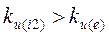 ). Такие соотношения между коэффициентами искажения форм кривых объясняются зависимостью реактивных сопротивлений от частоты:
). Такие соотношения между коэффициентами искажения форм кривых объясняются зависимостью реактивных сопротивлений от частоты: 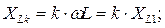
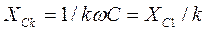 .
.
8. Измерение действующих значений несинусоидальных токов и напряжений
Для измерения действующих значений токов и напряжений в цепях переменного синусоидального тока применяются различные приборы, отличающиеся по принципу их действия или системой. Независимо от устройства шкалы всех приборов для измерения действующих значений токов и напряжений проградуированы в действующих значениях измеряемых величин.
Приборы непосредственного измерения (к таким относятся приборы электромагнитной и электродинамической систем) реагирует на действующее значение измерянной величины (I, U) и, следовательно, для их шкал коэффициент пересчета равен единице (кn=1) .
Приборы косвенного измерения могут реагировать на среднее (Iср, Uср) или на максимальное (Imax, Umax) значение измеряемой величины, но их показания пересчитываются к действующим значениям синусоидальных функций.
Для приборов, реагирующих на среднее значение, коэффициент пересчета равен:
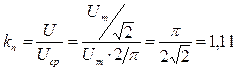
Для приборов, реагирующих на максимальное значение, коэффициент пересчета равен:
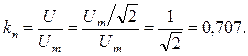
Действующее значение несинусоидальной функции зависит только от амплитуд отдельных гармоник, в то же время ее максимальное и среднее значения зависят как от амплитуд гармоник, так и от их фазовых сдвигов. Из этого следует вывод, что показания приборов косвенного измерения, реагирующих на максимальное или среднее значение, в цепях несинусоидального тока не будут соответствовать действующим значениям измеряемых величин.
Рассмотрим два примера. Пусть измеряемое напряжение содержит 1-ю и 3-ю гармоники, но с разными фазовыми сдвигами между ними:
a) 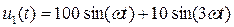 , (рис. 124а),
, (рис. 124а),
б) 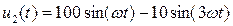 , (рис. 124б).
, (рис. 124б).
Действующие (U), максимальные (Umax) и средние (Uср) значения этих напряжений, рассчитанные математически по соответствующим формулам, а также показания приборов различных систем (V1 – непосредственного измерения, V2 - косвенного измерения с реакцией на максимальное значение Umax и V3 - косвенного измерения с реакцией на среднее значение Uср) приведены ниже в таблице.

| Схема | U, B | Umax, B | Ucp,B | V1 | V2 | V3 |
| а) | 71,1 | 65,8 | 71,1 | 63.6 | 73,0 | |
| б) | 71,1 | 61,6 | 71,1 | 77,8 | 68,4 |
Как видно из приведенных в таблице цифр, показания приборов косвенного измерения существенно зависят от фазового сдвига между гармониками, при этом методическая погрешность измерения может составлять значительную величину (в рассматриваемом примере около 10 %).
Дата добавления: 2020-07-18; просмотров: 719;











