Теоремы и методика их изучения в курсе геометрии средней школы

Теоремы и их виды

Связь между понятиями устанавливается с помощью суждений. Суждением принято называть предложение, в котором выражается мысль о предмете, объекте, явлении. Существуют два основных свойства суждения: что-то утверждать или отрицать, быть истинным или ложным.

Выделяются следующие виды суждений:

· общеутвердительное (образуется с помощью кванторных слов: всякий, любой);

· частно утвердительное (образуется с помощью кванторных слов: существуют, некоторые);

· общеотрицательное (образуется с помощью кванторных слов: ни один, никакой, не существует);

· частно отрицательное (образуется с помощью кванторных слов: не всякий, не любой).

Часто кванторные слова опускаются, считается, что они понятны из смысла всего предложения.

Например,

«все квадраты суть прямоугольники» - общеутвердительное суждение; «некоторые треугольники равнобедренные» - частно утвердительное суждение;

«не существует рационального числа, квадрат которого равен 2» - общеотрицательное суждение;

«не любое натуральное число – чётное» - частно отрицательное суждение.

Математическим предложением называют повествовательное предложение, выражающее общеутвердительное или общеотрицательное суждение о математических объектах.

Под теоремой принято понимать математическое предложение (утверждение), истинность которого доказывается.

Таким образом, родословную понятия «теорема» можно охарактеризовать «цепочкой» понятий: теорема→математическое предложение→ суждение.

Запись теоремы состоит из формулировки (суждения, утверждения) и доказательства.

Виды формулировки теоремы

Формулировка теоремы может быть категорической или условной. Для условной формы характерны слова «если…, то…». Например, «если в параллелограмме диагонали равны, то параллелограмм является прямоугольником». Теорема «сумма углов треугольника равна 180°» сформулирована в категорической форме.

В формулировке каждой теоремы можно выделить условие (то, что дано) и заключение (то, что требуется доказать). Если теорема сформулирована в условной форме, то между словами «если…, то» содержится её условие, после слова «то» - заключение. Пусть Р – условие теоремы, а Q – её заключение. Тогда символически теорему можно записать в виде Р Þ Q (если Р, то Q). При выделении условия и заключения в теореме, сформулированной в категорической форме, нет такой ясности. Поэтому целесообразно научить школьников переходить от условной к категорической формулировке теоремы. Так, приведённую выше теорему можно переформулировать: «если данная фигура – треугольник, то сумма его углов равна 180°».

Из данной теоремы (1) могут быть образованы ещё три утверждения. Поменяем местами условие и заключение. Получим обратное утверждение (2) Q Þ Р (если Q, то Р). Оно может быть истинным (тогда это обратная теорема) или ложным. Заменим условие и заключение теоремы на их отрицание. Получим противоположное утверждение (3) 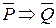(если не Р, то не Q). Оно также может быть либо истинным (теоремой), либо ложным. Наконец, может быть составлено контрапозитивное утверждение вида (4) .

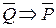Например, из теоремы «если углы вертикальны (Р), то они равны (Q)» (1) можно образовать следующие утверждения:

«если углы равны (Q), то они вертикальны (Р)» (2);

«если углы не вертикальны ( 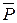), то они не равны ( 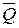)» (3);

«если углы не равны ( 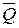),то они не вертикальны ( 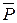)» (4).

Утверждения (1) и (4) истинны, а (2) и (3) – ложны. В математической логике доказывается, что утверждения (1) и (4), (2) и (3) равносильны, то есть их таблицы истинности совпадают. Схематически это можно изобразить так:

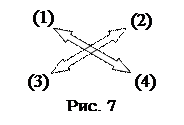
Аналогичным примером из алгебры является теорема «если каждое слагаемое делится на число, то и сумма делится на это число». Теорема «если в четырёхугольнике суммы противоположных сторон равны, то в него можно вписать окружность» служит примером истинности всех четырех утверждений.

Необходимое и достаточное условия

Пусть теорема сформулирована в виде Р Þ Q (если Р, то Q). Тогда Q называют необходимым условием Р, а Р – достаточным условием Q. Ясно, что Q – необходимое и достаточное условие Р, если обратное утверждение является истинным. Например, равенство углов является необходимым условием их вертикальности, а вертикальность углов является достаточным условием их равенства. При этом равенство углов не является необходимым и достаточным условием их вертикальности, так как обратное утверждение не является истинным. Равенство сумм противоположных углов четырёхугольника является необходимым и достаточным условием того, что в него можно вписать окружность. Подчёркивая этот факт, теорему формулируют в виде «для того, чтобы в четырёхугольник можно было вписать окружность необходимо и достаточно, чтобы суммы его противоположных сторон были равны». При этом доказывается истинность необходимого и достаточного условий. Доказывая необходимость, следует выделенное условие поставить в заключение теоремы.

Необходимость.

Дано: четырёхугольник; окружность, вписанная в четырёхугольник.

Доказать:суммы противоположных сторон четырёхугольника равны.

Затем докажем истинность обратной теоремы и тем самым докажем достаточность.

Достаточность.

Дано:суммы противоположных сторон четырёхугольника равны.

Доказать: в четырёхугольник можно вписать окружность.

Если некоторое условие Q является необходимым и достаточным условием Р, то его называют критерием Р. Так, равенство сумм противоположных сторон четырёхугольника является критерием того, что в него можно вписать окружность.