Классификация математических понятий

Объём математических понятий раскрывается с помощьюклассификации. Под классификацией понимают распределение объектов, принадлежащих объёму понятия, по классам (видам, типам). Основанием для такого распределения может быть некоторое существенное свойство, которым обладают не все объёкты, составляющие объём понятия. Например, свойство Р₁ «иметь тупой угол» позволяет выделить класс тупоугольных треугольников. Это свойство называется основанием классификации. Другой класс составят нетупоугольные треугольники (не Р₁) . Выберем иное основание классификации Р₂ теперь нетупоугольных треугольников: «иметь прямой угол». Новый класс составят прямоугольные треугольники. Оставшийся класс составят остроугольные треугольники. Изобразим полученную классификацию треугольников схематично.

Анализ проведённой классификации позволяет выявить её алгоритм:

1) выбирается основания классификации Р₁;

2) первый класс составляют элементы объёма понятия, обладающие свойством Р;

3) второй класс составляют элементы объёма понятия, не обладающие свойством Р₁;

4) далее процесс продолжается аналогично для оснований Р_1,…,Р_п

Приведём ещё один пример классификации алгебраических выражений. Напомним, что алгебраическим выражением называется выражение, содержащее только операции сложения, вычитания, умножения, деления, извлечения корня и возведения в степень с рациональным (в частности, с натуральным или целым) показателем.

Р₁ – содержит операцию извлечения корня (возведения в степень с рациональным показателем ).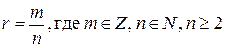

Р₂ – содержит операцию деления на выражение с переменной (возведение в степень с целым показателем).

Р₃ - содержит только операцию умножения (возведение в степень с натуральным показателем).

Условия правильной классификации

1. В основании классификации может быть использовано лишь общее свойство всех объектов.

Контрпример. Невозможна классификация геометрических фигур по основанию «содержит пару перпендикулярных сторон», так как наличие сторон не является общим свойством геометрических фигур.

2. На каждом этапе классификации может использоваться лишь одно основание. Получаемые классы не должны пересекаться.

3. Классификация должна быть полной, то есть каждый объект должен попасть в один и только один класс.

Наконец отметим, что каждое понятие может быть рассмотрено с 5 позиций (Н. Ф. Талызина):

1. Определение понятия.

2. Символическая запись.

3. Геометрическая интерпретация.

4. Свойства и признаки понятия.

5. Приложения понятия.

Охарактеризуем понятие производной с этих позиций.

1. Производной функции в точке х₀ называется предел отношения приращения функции к приращению аргумента, если приращение аргумента стремиться к 0.

2. .

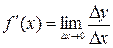3. Значение производной функции в точке х₀ равно угловому коэффициенту касательной, проведённой к графику этой функции в точке с абсциссой х₀.

4. Например, свойство «если функция дифференцируема в точке х₀, то она непрерывна в этой точке.

5. Приложения производной к отысканию промежутков монотонности, точек экстремума, наибольшего и наименьшего значений функции и другие.