Доказательство теоремы

Процесс доказательства является предметом изучения логики, Мы рассмотрим некоторые аспекты, относящиеся к доказательству теорем в школе.

Одним из основных элементов доказательства теорем является умозаключение. Умозаключение есть мыслительная операция, в результате которой из одного или нескольких суждений, находящихся в определённой смысловой взаимной связи, получается новое суждение. По отношению к исходным суждением оно содержит новое знание. Исходные суждения – это посылки, полученное новое суждение – это вывод.

При доказательстве теорем в школьном курсе математики наиболее часто используется умозаключение, называемое силлогизмом. Оно имеет следующее строение:

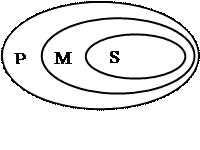
Все М суть Р (большая посылка)

Все S суть М (малая посылка)

S суть Р (вывод)

Рис. 8

Доказательство теоремы – это цепочка последовательно связанных силлогизмов, устанавливающих её истинность. При этом посылками силлогизмов могут быть аксиомы, теоремы, определения.

В качестве примера рассмотрим доказательство теоремы: «при пересечении двух параллельных прямых секущей соответственные углы равны».

Дано: а || b. c – секущая,

Доказать: Ð1=Ð2.

1 силлогизм:

Б.П.: Вертикальные углы равны.

М.П.: Ð1 и Ð3 –вертикальные.

В.: Ð1 = Ð3

2 силлогизм:

Б.П.: При пересечении двух параллельных прямых третьей внутренние накрест лежащие углы равны.

М. П.: Ð2 и Ð3 – внутренние накрест лежащие.

В.: Ð2 = Ð3

3 силлогизм.

Б.П. Если правые части равенства равны, то равны и левые части.

М.П.: Ð1 = Ð3, Ð2 = Ð3.

В.: Ð1=Ð2.

Существуют и другие правила вывода, например, отрицания,

контрапозиции.

Все доказательства можно разделить на прямые и косвенные. При прямом доказательстве задача состоит в том, чтобы подыскать такие утверждения, из которых по правилам вывода прийти к заключению теоремы. Доказательство, которое основывается на установлении истинности посредством опровержения некоторых суждений, называется косвенным. К косвенным доказательствам относится метод доказательства от противного или разделительный метод. Описание названных методов рассмотрите по учебному пособию [2, стр. 82].