СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ

Скорость – векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.

При векторном способе задания движения точки вектор скорости в данный момент времени равен производной от радиус – вектора точки по времени:

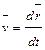. (7.2)

Вектор скорости направлен по касательной к траектории в сторону движения точки (рис. 7.3).

Рис. 7.3

При естественном способе задания движения точки вектор скорости определяется:

.

В этой зависимости производная 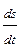представляет собой проекцию скорости v на касательную, т.е. определяет алгебраическую величину скорости. 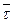- единичный вектор касательной, направленный в сторону возрастающих значений S. Вектор касательной всегда направлен в сторону увеличения координаты (рис. 7.4).

Определим скорость точки при задании ее движения координатным способом. Пусть заданы уравнения движения точки в виде:

; ; .

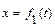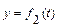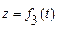Обозначим единичные векторы касательной (орты ) осей координат через

Рис. 7.4

Проведем из начала координат точки О в движущуюся точку М радиус вектор ОМ, тогда:

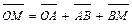или .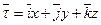

Скорость точки равна производной от радиус – вектора по времени. Найдем эту производную, учитывая, что орты 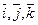имеют неизменные модули и направления и могут быть вынесены за знак производной.

.

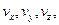Построив прямоугольный параллелепипед, оси которого параллельны осям координат, а диагональ совпадает со скоростью ,получим проекции скорости на оси координат равные алгебраическим значением отрезков Ma, Mb, Mc, тогда:

.

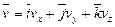Т.е. проекции скорости точки на неподвижные оси декартовых координат равны первым производным от соответствующих координат точки по времени.

При данном варианте задания движения точки её ускорение равно второй производной от радиус – вектора по времени

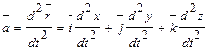. (7.3)

а с учетом того, что:

.

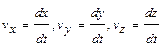Получим:

.

Таким образом, проекции ускорения точки на неподвижные оси координат равны вторым производным от соответствующих координат точки по времени или первым производным по времени от проекций скорости на соответствующие оси.

При задании движения векторным способом ускорение точки, характеризующее быстроту изменения модуля и направления скорости точки, равно первой производной от скорости или второй производной от радиус – вектора точки по времени:

.

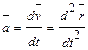При задании движения естественным способом, ускорение точки равно геометрической сумме двух векторов, один из которых направлен по главной нормали и называется нормальным ускорением , а другой направлен по касательной, и называется касательным ускорением точки 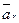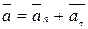(рис. 7.5).

Нормальное ускорение существует лишь при криволинейном движении точки М и характеризует изменение направления вектора скорости.

Рис. 7.5

Касательное ускорение существует лишь при неравномерном движении и характеризует изменение модуля скорости.