РАВНОУСКОРЕННЫЙ ПОДЪЕМ ГРУЗА

Рассмотрим вариант подъема груза с помощью троса длиной 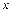(рис. 8.1).

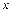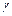На данной схеме – длина троса; – площадь поперечного сечения троса; – удельный вес материала троса; 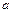– ускорение при подъеме (груз поднимается равноускоренно).

Рассмотрим действие динамической силы:

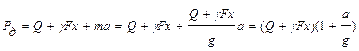. (8.1)

Статическое напряжение (при равномерном подъеме груза) определяется зависимостью:

Рис. 8.1

.

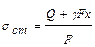Динамическое напряжение:

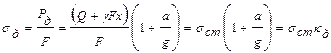, (8.2)

где 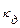– динамический коэффициент (не может быть меньше 1).

Таким образом, эффект динамического воздействия больше статического, а т.к. допускаемые напряжения не связаны с характером динамически сил, то:

.

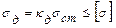РАСЧЕТ ОБОДА МАХОВИКА

Обод с радиусом 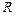(средний радиус) и площадью поперечного сечения обода 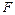вращается с угловой скоростью 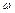. Влиянием спиц пренебрегаем (рис. 8.2).

Выделим бесконечно малый элемент обода длиной 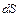(рис. 8.3). При движении сила инерции направлена от центра. Масса выделенного элемента может быть найдена по формуле:

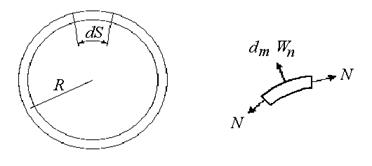
Рис. 8.2 Рис. 8.3.

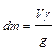, (8.3)

где 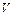– объем элемента, 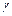– удельный вес материала обода.

Однако:

.

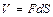После подстановки в формулу (8.3) получим:

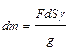. (8.4)

Как известно из курса теоретической механики нормальное ускорение может быть найдено по формуле

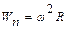. (8.5)

Запишем условие равновесия для половины обода маховика (рис. 8.4).

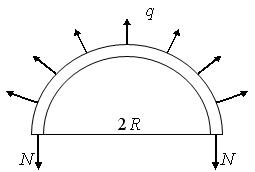
Рис. 8.4

Интенсивность действия распределенной нагрузки может быть найдена по формуле:

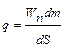. (8.6)

Подставим в выражение (8.6) выражения (8.4) и (8.5):

.

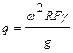Усилия 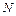противодействуют распределенной нагрузке, следовательно:

.

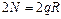Откуда:

.

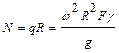Динамическое напряжение может быть определено по формуле:

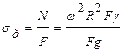. (8.7)