Уточненные расчеты на прочность при изгибе

При уточненных расчетах на прочность необходимо оценить влияние не только нормальных напряжений, но и касательных, при этом важно определить точку в поперечном сечении, в которой влияние этих напряжений наиболее значительно. Для этого необходимо научиться правильно строить эпюру касательных напряжений в поперечном сечении балки.

Рассмотрим случай построения эпюры касательных напряжений в прямоугольном поперечном сечении. Пусть в этом сечении действует поперечная сила 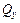(рис. 5.13).

Момент инерции сечения относительно горизонтальной оси 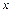определяется зависимостью

.

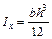Для определения величин касательного напряжения в точке 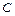необходимо провести через эту точку прямую, параллельную оси .

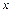Определим статический момент отсеченной части сечения (это произведение площади отсеченной части на расстояние от нейтральной оси до центра части отсеченной части):

.

	t

x

y

h

b

tmax

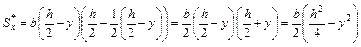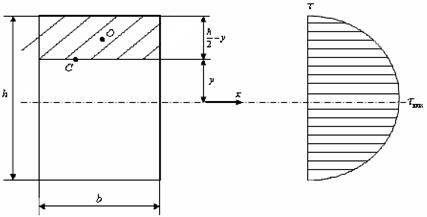
Рис. 5.13

Подставим в формулу касательных напряжений полученные выра-
жения:

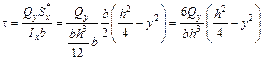. (5.11)

Из этого выражения следует, что касательные напряжения изменяются по закону квадратной параболы.

При 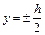напряжение 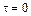. Наибольшее напряжение при 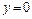, т.е. на нейтральной оси

.

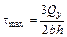Вопросы для самопроверки

К разделу 5

1. Какие внутренние усилия возникают в поперечном сечении при плоском изгибе?

2. Как вычисляется изгибающий момент в поперечном сечении по методу сечений?

3. Как вычисляется поперечная сила по методу сечений?

4. Какова дифференциальная зависимость между изгибающим моментом и распределённой нагрузкой?

5. Почему нормальные напряжения при чистом и поперечном изгибе определяются одинаково?

6. На каком законе основан вывод формулы Журавского?

7. Почему касательные напряжения в большинстве случаев не используются для оценки прочности при поперечном изгибе?

Кручение

Под деформацией кручения понимают деформацию стержня, при которой в поперечном сечении из всех внутренних усилий возникает только крутящий момент.

Метод сечений при кручении:крутящий момент в произвольном сечении бруса численно равен алгебраической сумме внешних скручивающих моментов, приложенных по одну сторону от сечения.

При расчетах на прочность и жесткость, знак крутящего момента не имеет принципиального значения, поэтому он может быть выбран произвольно, но его необходимо придерживаться до конца решения задачи.

Определение:Стержень, работающий на кручение, называется валом.