Определение нормальных напряжений при чистом изгибе

Рассмотрим случай возникновения чистого изгиба, т.е. когда в поперечном сечении действует только изгибающий момент .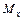

Так как 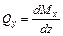, то на участке чистого изгиба 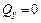, а изгибающий момент имеет постоянное значение. (Средняя часть балки) (рис. 5.6).

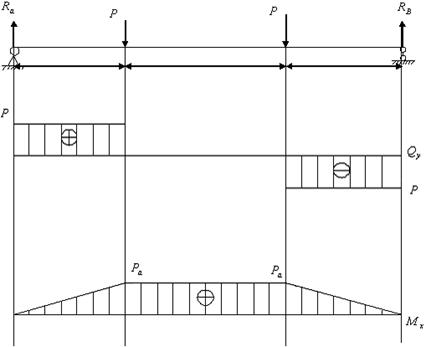
Рис. 5.6

Основные выводы из опытов на чистый изгиб

Разобьем элемент на ряд бесконечно малых полосок (рис. 5.7).

Каждый физический элемент (полоску) параллельную оси балки будем называть волокном.

1. При чистом изгибе часть волокон испытывает деформацию простого растяжения, а другая часть – простого сжатия. Волокна, расположенные между ними и не испытывающие деформаций удлинения, называются нейтральными волокнами.

2. Соседние волокна не оказывают давления друг на друга.

3. Гипотеза плоских сечений. Поперечные сечения в процессе деформации остаются плоскими и только поворачиваются вокруг оси, расположенной в нейтральном слое (вокруг нейтральной оси).

Рис. 5.7

Следствие: Волокна, равноотстоящие от нейтрального слоя, деформируются одинаково.

Выделим из балки, находящейся в условиях чистого изгиба, бесконечно малый элемент длиной 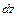сечениями, перпендикулярными оси балки (рис. 5.8).

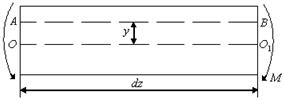
Рис. 5.8

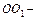нейтральное волокно в недеформируемом состоянии:

.

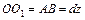Под воздействием момента 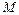произойдет деформация элемента
(рис. 5.9). Согласно первому выводу из опытов на чистый изгиб нейтральное волокно не деформируется и необходимо определить деформацию волокна 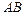находящегося на расстоянии 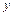от нейтральной оси.

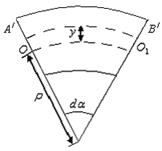
Рис. 5.9

Относительная деформация волокна AB:

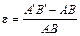, (5.3)

где 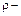радиус кривизны нейтрального волокна.

.

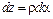Тогда ;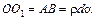

.

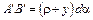Подставим полученные выражения в уравнение (5.3):

.

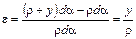Согласно закону Гука,

.

Тогда

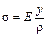(5.4)

физическое уравнение совместности деформаций. (Закон распределения напряжений по высоте балки).

Свяжем напряжение 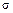с внутренними силовыми факторами, возникающими в поперечном сечении при чистом изгибе. Пусть на бесконечно малый элемент, находящийся на расстояни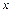и и 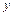от соответствующих осей, действует напряжение 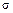(рис. 5.10).

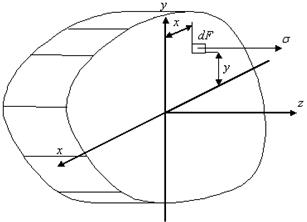
Рис. 5.10

Запишем уравнение равновесия в виде суммы проекций на оси координат.

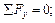
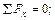
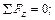
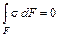. (5.5)

Уравнение моментов относительно осей:

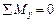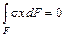; ; (5.6)

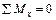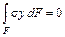; ; (5.7)

.

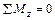Будем решать совместно уравнения (5.4) – (5.7), подставляя уравнение (5.4) в уравнения (5.5) – (5.7) последовательно:

.

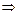
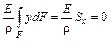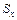равен нулю, так как ос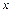и и – центральные;

,

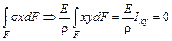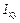равен нулю, согласно свойству главных центральных осей;

,

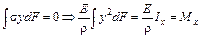или .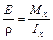

Подставим в уравнение (5.4):

.

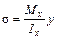Общий вид эпюры нормальных напряжений при изгибе показан на рис. 5.11.

	smax

ymax

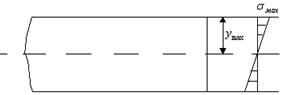
Рис. 5.11

В данной формуле 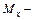изгибающий момент в сечении; 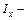осевой момент инерции сечения относительно главной центральной оси 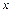; 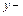расстояние от рассматриваемой точки сечения до нейтральной оси. Данная зависимость линейная. Максимальное напряжение возникает в точках, наиболее удаленных от нейтральной оси:

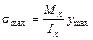. (5.8)