Касательные напряжения при изгибе

При чистом изгибе в поперечном сечении бруса действует только изгибающий момент и, следовательно, возникают только нормальные напряжения.

В случае поперечного изгиба в сечении бруса действуют наряду с изгибающими моментами перерезывающие силы 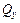. В связи с этим в поперечных сечениях возникают не только нормальные напряжения, но и касательные напряжения 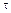. Их возникновение сопровождается появлением угловых деформаций, поэтому каждая элементарная площадка получает угловые смещения, обусловленные сдвигом.

Касательные напряжения распределены по сечению неравномерно, поэтому угловые смещения также распределяются по сечению неравномерно. В связи с этим при поперечном изгибе, в отличие от чистого изгиба, поперечные сечения не остаются плоскими.

Однако на величине нормальных напряжений искажение плоскости поперечных сечений сказывается незначительно, поэтому гипотезу плоских сечений можно считать применимой и при поперечном изгибе.

в)

б)

а)

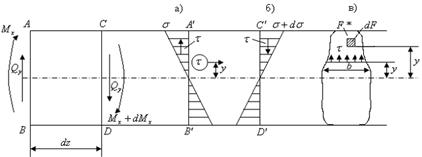
Рис. 5.12

Определим приблизительно касательные напряжения при поперечном изгибе. Для этого выделим из бруса элемент длиной .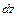

На левую часть элемента действует изгибающий момент 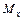, на правую – изгибающий момент 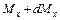, а также перерезывающая сила 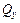. В левой части сечения действует нормальное напряжение 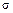и касательное 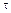(рис. 5.12, а). На правую часть сечения действует нормальное напряжение 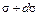и касательное 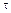(рис. 5.12, б).

Повернутое на 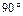левое сечение ("лицом" к нам) показано на
рис. 5.12, в. Разделим элемент на рис. 5.12, в продольным горизонтальным сечением, проведенным на расстоянии 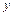от нейтральной оси, и рассмотрим условие равновесия верхней отсеченной части.

Равнодействующая нормальных сил в левом сечении в пределах отсеченной части 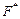определяется как сумма проекций на ось 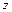(см. вывод формулы нормальных напряжений):

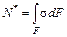. (5.9)

Однако, зная что

,

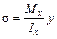то после подстановки в уравнение (4.9), получим

,

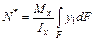где 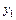– текущая ордината площадки .

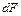Полученный интеграл – статический момент относительно горизонтальной оси части площади, расположенной выше продольного сечения (выше уровня 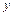). Обозначим его величину через 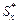. Тогда,

.

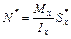В правом сечении продольная сила определяется зависимостью

.

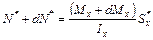Разность этих двух усилий

.

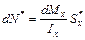Она должна уравновешиваться касательными силами, возникающими в продольном сечении элемента 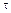. Если считать, что они распределяются по ширине сечения равномерно, то

,

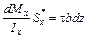или формула Журавского

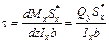. (5.10)

Данное выражение позволяет вычислять касательное напряжение, возникающее в продольном сечении стержня, а также в его поперечном сечении (с учетом закона парности касательных напряжений).

Закон парности касательных напряжений: по двум взаимно перпендикулярным площадкам действуют равные по величине и противоположные по направлению касательные напряжения.

Зависимость от расстояния до нейтральной оси, представленная в формуле Журавского, не носит линейного характера, так как она представлена в неявном виде в величине 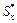, поэтому характер изменения касательных напряжений по высоте балки криволинеен. В каждом конкретном случае для вычисления величины 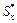необходимо научиться определять значения этого параметра в зависимости от расстояния до нейтральной оси.

По формуле (5.10) определяется лишь абсолютное значение касательного напряжения; знак этого напряжения совпадает со знаком перерезывающей силы, действующей в рассматриваемом сечении.