Моменты инерции простейших сечений

1. Прямоугольник.

Рассмотрим прямоугольник с высотой h и основанием b относительно осей, проходящих через его центр тяжести (рис. 4.4).

Выделим из прямоугольника линиями, параллельными оси z, элементарную полоску с высотой dy и шириной b. Площадь этой элементарной полоски

.

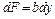Подставив полученное значение в зависимость (3.5) вместо dF, получим

.

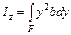Пределы интегрирования по оси y будут изменяться от 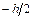до :

.

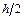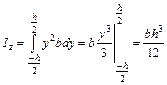Аналогично:

.

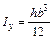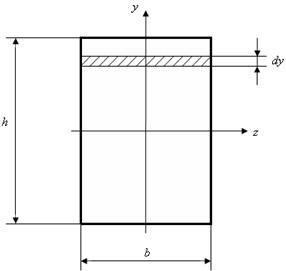
Рис. 4.4

Центробежный момент инерции относительно этих осей равен нулю, так как они – главные.

2. Треугольник.

Рассмотрим равнобедренный треугольник с основанием b и высотой h (рис. 4.5).

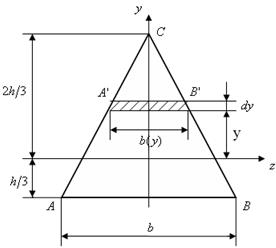
Рис.4.5

Для него центр тяжести расположен на расстоянии 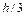от основания. Выделим из него линиями, параллельными оси z на расстоянии y от этой оси, элементарную полоску высотой dy. Основание этой полоски рав-
но b(y).

Треугольники ABC и 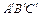подобные:

.

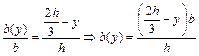Площадь элементарной полоски

.

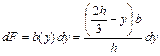Согласно определению

.

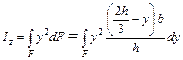Пределы интегрирования по оси y будут изменяться от 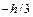до :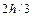

.

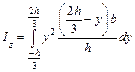Умножим числитель и знаменатель подынтегрального выражения на 3:

.

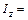
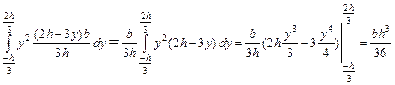Данное выражение справедливо и для неравнобедренного треугольника.

3. Круг.

Определим полярный момент инерции круга (рис. 4.6).

Выделим из круга двумя кольцевыми сечениями с радиусами p и
p + dp элементарное кольцо. Площадь его будет равна

.

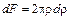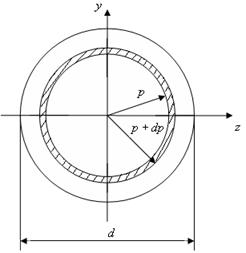
Рис. 4.6

Согласно определению:

.

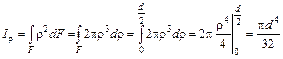Так как круг – фигура симметричная, то

.

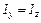Однако, в соответствии с (4.6).

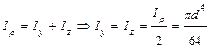
Вопросы для самопроверки

К разделу 4

1. Почему геометрические характеристики плоских сечений, кроме площади, называют моментами?

2. Чему равен статический момент относительно центральной оси?

3. С чего начинается вычисление координат центра тяжести любой фигуры?

4. Как вычисляются моменты инерции прямоугольника относительно центральных осей, параллельных сторонам прямоугольника?

5. Можно ли при определении моментов инерции сложных фигур вычислять не сумму, а разность моментов инерции простых фигур?

Изгиб

Общие понятия

При центральном растяжении-сжатии и кручении прямых брусьев их оси остаются прямыми и после возникновения деформаций. В отличие от этих видов нагружения при изгибе происходит искривление осей прямых брусьев.

I. Классификация по наличию действующих силовых факторов:
а) чистый изгиб, когда в поперечном сечении бруса действует только изгибающий момент; б) поперечный изгиб, когда наряду с изгибающим моментом действует перерезывающая сила.

II. По направлению воздействия внешних силовых факторов: а) прямой изгиб, когда плоскость действия внешних сил и моментов совпадает с плоскостью, проходящей через одну из главных центральных осей инерции сечений; б) косой изгиб, когда плоскость действия внешних сил и моментов не совпадает с плоскостями, проходящими через одну из главных центральных осей инерции сечения.

Определение: Стержень, преимущественно работающий на изгиб, называется балкой.

Частный вид балки – консоль, когда один ее конец жестко закреплен (рис. 5.1).

Внешние силовые факторы при изгибе:

1. сосредоточенная сила (поперечная, перерезывающая) Р, т; кг; Н;

2. изгибающий момент М, т×м;

3. распределенная нагрузка q, Н/м.

Правило знаков:поперечная сила Q_y в произвольном сечении численно равна сумме проекций всех внешних сил, действующих по одну сторону от проведенного сечения на ось, перпендикулярную оси балки. Q_y положительна, если внешние силы стремятся повернуть рассматриваемую часть относительно центра тяжести проведенного сечения по часовой стрелке (рис. 5.2).

Рис. 5.1

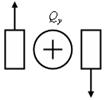Рис. 5.2

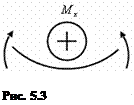Изгибающий момент 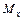в произвольном сечении численно равен алгебраической сумме моментов всех внешних сил, действующих по одну сторону от сечения относительно центра тяжести этого сечения. 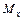положителен, если балка изгибается выпуклостью вниз (рис. 5.3).