Геометрические характеристики плоских сечений

Статические моменты и моменты инерции сечений

Поперечное сечение бруса можно охарактеризовать его размерами и площадью сечения.

Площадь – простейшая геометрическая характеристика поперечного сечения.

Если представить сечение состоящим из бесчисленного множества элементарных площадок dF (рис. 4.1), то площадь всего сечения

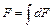, см². (4.1)

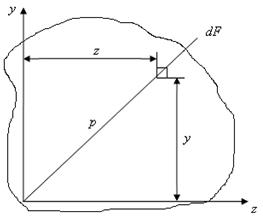
Рис. 4.1

Однако, две фигуры, например круг и квадрат, с одинаковой площадью по-разному воспринимают действие изгибающей нагрузки и крутящего момента.

Для более полной характеристики сечения вводится понятие моментов. Выражения этих характеристик отличаются от выражения (3.1) тем, что у них под знак интеграла входят произведения элементарных площадок на функции координат этих площадок (y, z, p). Таким образом, указанные геометрические характеристики зависят не только от формы и размеров сечения, но и от положения осей и полюсов, относительно которых они вычисляются.

Определение: Статическим моментом сечения относительно некоторой оси называется, взятая по всей его площади F, сумма произведений элементарных площадок dF на их расстояние до этой оси.

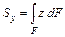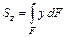; , см³.

Свойство: Статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси.

Найдем зависимость между статическими моментами одного и того же сечения относительно параллельных осей z и 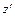(рис. 4.2). В соответствии с определением

; .

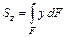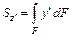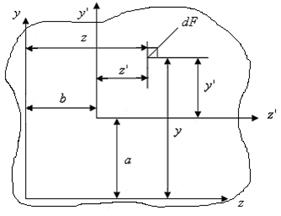
Рис. 4.2

Однако, согласно построению:

;

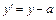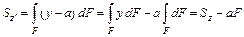. (4.2)

Аналогично:

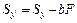. (4.3)

Определим положение осей y₁ и z₁ , относительно которых статические моменты равны нулю (рис. 4.3).

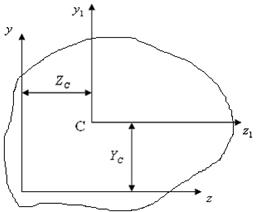
Рис.4.3

Для этого приравняем к нулю выражения (4.2) и (4.3):

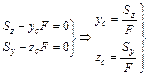. (4.4)

Точка пересечения осей y₁ и z₁ (точка С) является центром тяжести сечения.

Оси, проходящие через центр тяжести сечения, называются центральными осями.

Свойство центральных осей: относительно любой оси, проходящей через центр тяжести сечения, статический момент равен нулю.

Формулы (3.4) используют для определения положения центра тяжести сечения.

Определение: Осевым (экваториальным) моментом инерции сечения относительно некоторой оси называется, взятая по всей его площади F, сумма произведений элементарных площадок dF на квадраты их расстояний от этой оси.

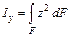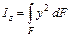; , см⁴. (4.5)

Центробежный момент инерции

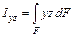, м⁴.

Полярный момент инерции

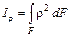, м⁴.

Если полюс при составлении полярного момента инерции совпадает с началом координат, то в соответствии с рис. 3.1:

.

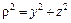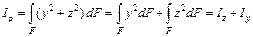, (4.6)

т.е. сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей, равна полярному моменту инерции этого сечения относительно точки пересечения указанных осей.