Статически неопределимые стержневые системы
План решения статически неопределимых задач:
1. Составляем уравнения равновесия (3.18).
2. Определяем степень статической неопределимости.
3. Из чисто геометрических соображений составляем геометрическое уравнение совместности деформаций (3.19).
4. Пользуясь физическими законами, выражаем деформации, вошедшие в уравнение (3.19) через внутренние усилия и внешние силы (3.21).
5. Составляем физическое уравнение совместности деформаций. Для этого уравнение (3.21) подставляем в уравнение (3.19) и получаем зависимость (2.25).
6. Решаем совместно уравнения (3.19) и физическое уравнение совместности деформаций (3.22).
Пример. Жесткий брус 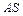 соединен с жесткой опорой посредством шарнира в точке S. К нему прикреплены два стержня 1 и 2, также соединенные с опорой. К конструкции приложена внешняя сила P (рис. 3.7). Раскрыть статическую неопределимость от действия внешней нагрузки.
соединен с жесткой опорой посредством шарнира в точке S. К нему прикреплены два стержня 1 и 2, также соединенные с опорой. К конструкции приложена внешняя сила P (рис. 3.7). Раскрыть статическую неопределимость от действия внешней нагрузки.
1.Составление расчетной схемы (рис. 3.8):
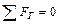 ;
; 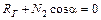 ;
;
 ;
; 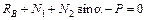 ;
;
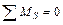 ;
; 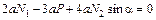 . (3.18)
. (3.18)
|
|
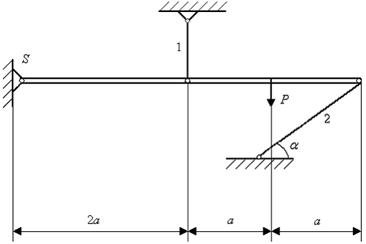
Рис. 3.7
Степень статической неопределимости равна единице:
|
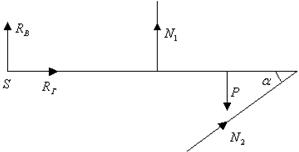
Рис. 3.8
Из уравнения (3.18) необходимо определить правильность направления реакций 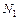 и
и 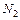 .
.
Для симметричных схем: направления проекций на вертикальную ось реакций 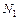 и
и 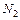 и внешней силы P должны иметь разные знаки.
и внешней силы P должны иметь разные знаки.
Для остальных схем: знаки моментов, создаваемых усилиями 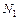 и
и 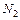 , и внешней силой P в уравнении моментов относительно опоры должны быть противоположными.
, и внешней силой P в уравнении моментов относительно опоры должны быть противоположными.
2.Составление схемы деформации (рис. 3.9).
1) Показываем положение схемы в исходном положении:
|
|
|
|
|
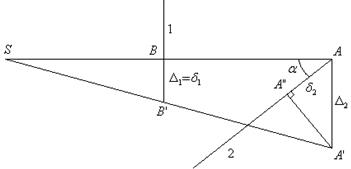
Рис. 3.9
2) Определяем, куда сместится жесткая балка от воздействия внешней силы, и показываем новое положение системы. При этом необходимо сделать два допущения:
а) жесткая балка не деформируется;
б) перемещение точек приложения стержней A и B происходит не по дугам окружностей, а строго вертикально.
Вертикальные перемещения точек приложения стержней обозначим через  и
и 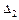 .
.
3) Из вновь полученных точек 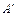 и
и 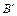 опускаем перпендикуляры на линии действия стержней в исходном состоянии. Обозначим деформации стержней через
опускаем перпендикуляры на линии действия стержней в исходном состоянии. Обозначим деформации стержней через 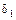 и
и 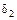 .
.
4) Находим соответствие между вертикальными перемещениями 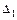 и
и 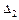 (для симметричных схем – из условия неразрывности конструкции; для других схем – из подобия треугольников):
(для симметричных схем – из условия неразрывности конструкции; для других схем – из подобия треугольников):
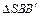 ~
~ 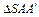 :
:
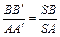 ;
;
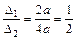 . (3.19)
. (3.19)
5) Выражаем вертикальные перемещения 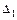 и
и 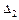 через
через 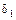 и
и 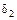 :
:
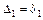 ;
;
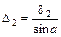 ;
;
Подставим полученные выражения в уравнение (3.19):
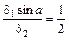 ;
;
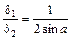 . (3.20)
. (3.20)
3.Выражаем деформации стержней через внутренние усилия в них (закон Гука):
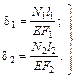 (3.21)
(3.21)
4.Составляем физическое уравнение совместности деформаций, подставив уравнение (3.21) в уравнение (3.20):
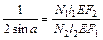 . (3.22)
. (3.22)
Длины стержней 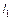 и
и 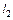 известны. Если дано соотношение площадей
известны. Если дано соотношение площадей 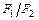 , используя его, сокращаем площади.
, используя его, сокращаем площади.
Получено недостающее уравнение. Решая его совместно с уравнением (2.21), можно определить усилия 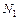 и
и 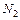 .
.
5.После определения 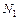 и
и 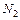 рассчитывают площади
рассчитывают площади 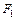 и
и 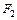 в соответствии с соотношением, через
в соответствии с соотношением, через 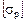 и
и 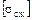 .
.
6.Производим проверку правильности решения.
1) В определенном масштабе откладываем длину бруса SBA (рис. 3.10).
2) В точках приложения стержней проводим их линии действия.
3) Откладываем вертикальные перемещения стержней в направлении, соответствующем схеме деформаций (в другом масштабе).
|
|
|
|
|
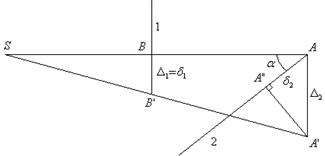
Рис. 3.10
Первая проверка:соединяем точки S, 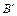 и
и 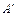 . Полученная линия должна быть прямой, а не ломаной линией.
. Полученная линия должна быть прямой, а не ломаной линией.
Вторая проверка: из полученных точек 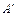 и
и 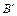 проводим перпендикуляры на линии действия стержней в исходном состоянии. Получаем точки
проводим перпендикуляры на линии действия стержней в исходном состоянии. Получаем точки 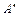 и
и 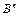 . Измеренные величины
. Измеренные величины 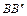 и
и 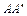 должны быть равны рассчитанным величинам
должны быть равны рассчитанным величинам 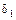 и
и 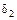 в выбранном масштабе деформации.
в выбранном масштабе деформации.
3.5. Напряжения, возникающие в стержневых системах от
неточности изготовления и температурных деформаций
Если хотя бы один из стержней шарнирно-стержневой системы выполнен не точно, т.е. его длина оказалась выше или ниже рассчитанной, то при сборке такой системы необходимо приложить дополнительные усилия. При этом все стержни системы после сборки будут подвергаться определенному силовому воздействию, даже при отсутствии внешних сил.
Если по условиям работы шарнирно-стержневой системы, выполненной точно, хотя бы один из стержней работает в условиях нагрева или охлаждения, то при этом происходит изменение его первоначальной длины (при нагреве – удлинение, при охлаждении – уменьшение первоначальной длины).
При решении подобных задач необходимо вначале определить величину температурной деформации, которая вычисляется по формуле
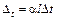 ,
,
где 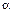 – коэффициент линейного расширения материала стержня;
– коэффициент линейного расширения материала стержня; 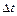 – перепад температур (может быть как > 0, так и < 0);
– перепад температур (может быть как > 0, так и < 0); 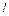 – длина стержня.
– длина стержня.
После определения температурной деформации данная задача решается подобно задачам, связанным с неточностью изготовления стержней.
Пример:В шарнирно-стержневой системе, состоящей из жесткого бруса и двух стержней, первый стержень выполнили короче на величину 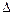 (рис. 3.11). Раскрыть статическую неопределимость от неточности изготовления.
(рис. 3.11). Раскрыть статическую неопределимость от неточности изготовления.

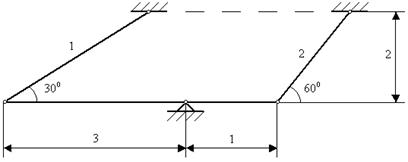
Рис. 3.11
1. Составление расчетной схемы (рис. 3.12).
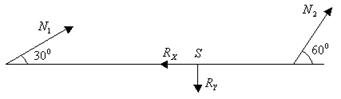
Рис. 3.12
Так как первый стержень выполнен короче, то при сборке системы его необходимо растянуть, т.е. внешнее усилие, приложенное к стержню – растягивающее. Реакция в этом стержне должна быть противоположна внешнему усилию.
Реакция во втором стержне должна уравновешивать реакцию в первом стержне.
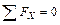 ,
, 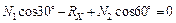 ;
;
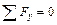 ,
, 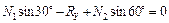 ;
;
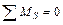 ,
, 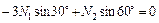 . (3.23)
. (3.23)
Проведем проверку правильности направления реакций:
Для симметричных схем: в уравнении проекции на вертикальную ось знаки реакций должны быть противоположными.
Для остальных схем: если имеется уравнение моментов, то знаки моментов должны быть противоположными.
Степень статической неопределимости равна единице.
2. Составление схемы деформаций (рис. 3.13).
1) Изображаем схему в исходном состоянии.
2) Мысленно отбрасываем стержень, выполненный точно (второй стержень). Так как первый стержень выполнен короче, то вертикальное перемещение точки 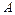 откладываем вверх.
откладываем вверх.
3) Опустим из точки 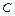 перпендикуляр на линию действия стержня в исходном состоянии. Получим точку
перпендикуляр на линию действия стержня в исходном состоянии. Получим точку 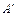 .
.
4) Проведем прямую 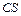 и опустим вертикаль из точки
и опустим вертикаль из точки 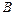 . Получим точку
. Получим точку 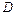 . Если бы отсутствовал стержень 2, то брус занял бы положение
. Если бы отсутствовал стержень 2, то брус занял бы положение 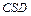 .
.
5) Так как стержень 2 реально присутствует и оказывает влияние на стержневую систему, то под его воздействием брус займет какое-то среднее положение между нейтральным 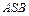 и крайним
и крайним  .
.

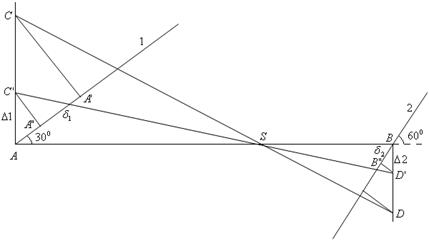
Рис. 3.13
Положение  – реальное положение жесткого бруса. Реальное вертикальное перемещение первого стержня
– реальное положение жесткого бруса. Реальное вертикальное перемещение первого стержня  , второго стержня –
, второго стержня – 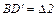 .
.
6) Опустим перпендикуляры из точек реального положения бруса  и
и 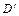 на линии действия стержней в исходном состоянии. Получим точки
на линии действия стержней в исходном состоянии. Получим точки 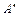 и
и 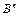 . При этом деформация второго стержня
. При этом деформация второго стержня 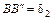 , второго стержня
, второго стержня 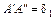 .
.
Стержень 1 реально удлиняется при сборке на величину 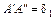 , так как его первоначальное положение после изготовления оканчивалось в точке
, так как его первоначальное положение после изготовления оканчивалось в точке 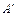 .
.
7) Ищем связь между вертикальными перемещениями 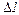 и
и 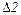 (подобно предыдущему разделу):
(подобно предыдущему разделу):
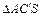 ~
~ 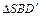 :
:
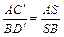 ;
;
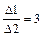 . (3.24)
. (3.24)
8) Выражаем вертикальное перемещение через деформации в стержнях.
Из 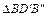 и
и 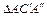 :
:
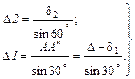 (3.25)
(3.25)
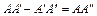 .
.
Подставим (3.25) в (3.24):
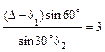 ;
;
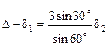 ;
;
 . (3.26)
. (3.26)
3. Составление физического уравнения совместности деформаций:
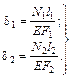 (3.27)
(3.27)
Подставим (3.27) в (3.26):
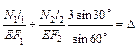 . (3.28)
. (3.28)
В подобных задачах площади 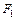 и
и 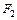 – заданы. Решая совместно уравнения (3.28) и (3.23) определим реакции
– заданы. Решая совместно уравнения (3.28) и (3.23) определим реакции 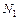 и
и 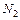 .
.
4. Произведем проверку правильности решения.
1) Откладываем брус 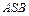 в определенном масштабе. В точках приложения стержней проводим их линии действия (рис. 3.13).
в определенном масштабе. В точках приложения стержней проводим их линии действия (рис. 3.13).
2) Откладываем вертикальные перемещения 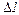 и
и 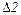 в направлениях, соответствующих схеме деформаций (в масштабе деформаций).
в направлениях, соответствующих схеме деформаций (в масштабе деформаций).
Первая проверка: линия 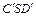 должна быть прямой.
должна быть прямой.
3) Из точек 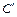 и
и 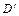 опускаем перпендикуляры на линии действия стержней.
опускаем перпендикуляры на линии действия стержней.
Вторая проверка: измеренные величины 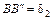 ,
, 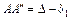 должны равняться рассчитанным значениям в соответствующем масштабе деформаций.
должны равняться рассчитанным значениям в соответствующем масштабе деформаций.
Дата добавления: 2020-07-18; просмотров: 618;











