ВНУТРЕННИЕ УСИЛИЯ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ СТЕРЖНЕЙ. МЕТОД СЕЧЕНИЙ
Элементы сооружений и конструкций представляют собой тела различных размеров и форм, выполненные из твердых деформируемых материалов. Под действием внешних сил эти тела деформируются, т.е. меняют свои первоначальные размеры и форму. Вследствие деформации первоначальные расстояния между частицами тела изменяются, и в материале появляются дополнительные силы внутреннего взаимодействия частиц. Именно от величины и характера распределения этих дополнительных сил внутреннего взаимодействия зависит надежность работы сооружения. Поэтому необходимо в первую очередь научиться определять эти силы, называемые в дальнейшем внутренними усилиями или внутренними силовыми факторами для расчетов сооружения и его элементов на прочность, жесткость и устойчивость.
В курсе "Сопротивление материалов" основным объектом всех расчетов, как правило, является стержень. Под стержнем или брусом понимают тело, один размер которого значительно больше двух других.
Если площадь поперечного сечения А по длине бруса постоянна, а линия, соединяющая центры тяжестей сечения прямая, то стержень называется прямым призматическим.
В общем случае площадь сечения А может непрерывно или ступенями изменяться вдоль продольной оси стержня, а продольная ось может иметь как прямолинейные, так и криволинейные участки.
Для определения внутренних усилий используется метод сечений. Рассмотрим суть этого метода на примере с прямым призматическим стержнем.
Пусть требуется определить внутренние усилия в произвольном сечении а–абруса, находящегося в равновесии в пространстве под действием системы внешних сил Fi (рис. 2.1а).
Мысленно рассечем стержень (брус) в сечении а–аплоскостью "С", перпендикулярной продольной оси, отбросим одну часть, например часть "В", и рассмотрим оставшуюся (в данном случае левую) часть "А". Рассматриваемая часть "А" будет находиться в равновесии, если к ней приложить систему усилий, распределенных по площади сечения. Эти усилия, заменяющие действие отброшенной части на рассматриваемую и есть внутренние усилия в сечении а–а. Согласно закону о равенстве действия и противодействия, внутренние усилия, которые приложены к части "А" в сечении а–а,равны и противоположны по направлению внутренним усилиям, действующим на часть "В" в том же сечении.
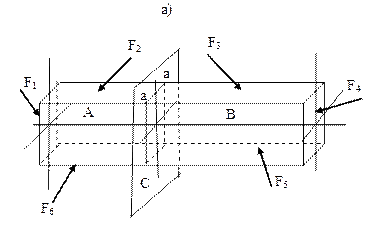
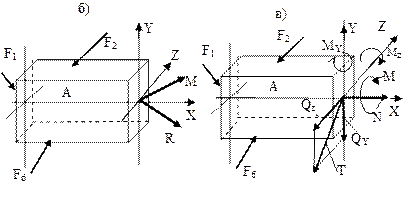
Рис. 2.1
В теоретической механике показано, что любая система сил, (в том числе и внутренних усилий, распределенных по какому-то закону по площади поперечного сечения а–а),может быть приведена к главному вектору R и вектору главного момента М. За центр приведения может быть выбрана любая точка поперечного сечения. В сопротивлении материалов за эту точку целесообразно принимать центр тяжести поперечного сечения
Сила R называется главным вектором, а момент М – главным моментом системы внутренних сил, действующих в данном сечении (рис. 2.1б).
Главный вектор R раскладывается на две составляющие силы: силу N, направленную вдоль оси бруса и называемую продольной силой, и силу Т, действующую в плоскости поперечного сечения и называемую поперечной силой (рис. 2.1в).
Главный момент М раскладывается на три составляющих момента: момент МХ = Мt, действующий в плоскости поперечного сечения (относительно продольной оси бруса Х) и называемый крутящим моментом, и моменты МZ и МY, действующие относительно двух взаимно перпендикулярных осей Z и Y, проходящих через центр тяжести сечения, лежащих в плоскости поперечного сечения, и называемые изгибающими моментами.
В дальнейшем более удобно для расчетов силу Т разложить на две составляющие ее поперечные силы QZ и QY, параллельные двум взаимно перпендикулярным осям, расположенным в плоскости поперечного сечения бруса (рис. 2.1в). Причем при расчетах на прочность оси Z и Y должны совпадать с главными центральными осями инерции поперечного сечения, о которых будет сказано далее в главе 5. Таким образом, в плоскости поперечного сечения в общем случае силы взаимодействия частей А и В между собой характеризуются шестью составляющими внутренних силовых факторов (или внутренних усилий): N – продольная (осевая) сила, QY и QZ – поперечные силы, МХ = Мt – крутящий момент, МZ и МY – изгибающие моменты.
Числовые значения этих сил нетрудно найти из шести уравнений равновесия для рассматриваемой части стержня с приложенными к ней приведенными выше внутренними усилиями:
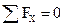 ; N +
; N + 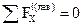 ;
;
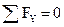 ; QY +
; QY + 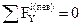 ;
;
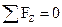 ; Qz +
; Qz + 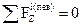 ;
;
 ; MX +
; MX + 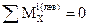 ;
;
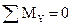 ; MY +
; MY + 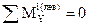 ;
;
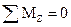 ; MZ +
; MZ + 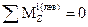 .
.
В каждое из этих уравнений будет входить только по одному неизвестному внутреннему усилию, которое легко определить. В верхнем индексе буквы лев означают, что суммируются проекции сил и моменты сил, действующих слева от сечения.
В некоторых случаях часть составляющих внутренних усилий будет равняться нулю, в зависимости от этого различают и виды деформаций:
– если в сечении имеется отличная от нуля только продольная сила N, а остальные внутренние силы равны нулю – имеет место один из простых видов сопротивления – центральное растяжение–сжатие;
– если отличным от нуля является только крутящий момент, а остальные внутренние силы равны нулю, то имеет место другой вид простого сопротивления – кручение;
– если отличными от нуля являются поперечная сила QY и изгибающий момент МZ , а остальные внутренние усилия равны нулю имеет место тоже один из простых видов сопротивления – прямой изгиб (при условии, что оси Z и Y являются главными осями инерции и центр тяжести совпадает с центром изгиба).
Правила знаков для внутренних усилий и примеры практического использования метода сечений при определении внутренних усилий рассмотрим в последующих главах при названных видах простых сопротивлений с определением внутренних усилий в сечениях стержней, построением их эпюр и дальнейшим расчетом их на прочность.
Дата добавления: 2021-12-14; просмотров: 572;











