Спектральний аналіз оцінки технічного стану електронної апаратури
План лекції
1. Аналітичне представлення гармонійних функцій.
2. Класифікаційний аналіз рядів Фур’є.
3. Практичне застосування методу спектрального аналізу.
На практиці для оцінки технічного стану безперервних блоків електронної апаратури (ЕА) часто використовують метод, який базується на теорії швидких перетворень Фур’є. Розглянемо більш детально зазначений метод. Періодичну функцію може бути подано у вигляді
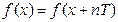 , (7.1)
, (7.1)
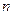 – будь-яке ціле число позитивне чи від’ємне,
– будь-яке ціле число позитивне чи від’ємне, 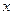 – будь-яка змінна величина, яка характеризує функцію.
– будь-яка змінна величина, яка характеризує функцію.
Хвиля напруги, яка вимірюється під час оцінки технічного стану може бути графічно представлена як функція 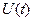 на рис. 7.1.
на рис. 7.1.
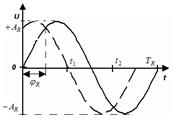
Рис. 7.1. Графік періодичної функції
Аналітично графічну залежність на рис.1 можна подати
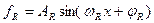 , (7.2)
, (7.2)
де 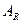 – амплітуда,
– амплітуда, 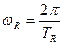 – циклічна частота,
– циклічна частота, 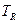 – довжина хвилі (період),
– довжина хвилі (період), 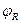 – фазовий здвиг. Отже маємо періодичну функцію (7.2). Як відомо, будь-яку періодичну функцію
– фазовий здвиг. Отже маємо періодичну функцію (7.2). Як відомо, будь-яку періодичну функцію 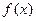 можна аналітично подати у вигляді суми деякого постійного члена і графічно у вигляді елементарних хвиль сигналу, а саме:
можна аналітично подати у вигляді суми деякого постійного члена і графічно у вигляді елементарних хвиль сигналу, а саме:
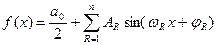 , (7.3)
, (7.3)
або у вигляді еквівалентного рівняння:
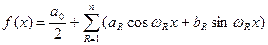 , (7.4)
, (7.4)
де 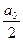 – середнє значення періодичної функції для всіх точок періоду
– середнє значення періодичної функції для всіх точок періоду 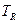 .
.
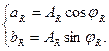 (7.5)
(7.5)
Тригонометричні ряди (3) і (4) будуть відповідати властивостям періодичності функцій лише у тому випадку, якщо циклічні частоти 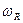 є кратними першій частоті
є кратними першій частоті  , тобто:
, тобто: 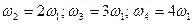 і т.п.
і т.п.
Тому ряди (3) і (4) можна записати у вигляді:
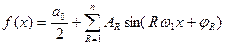 ; (7.6)
; (7.6)
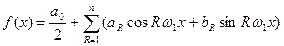 . (7.7)
. (7.7)
Ряди у вигляді (7.6) і (7.7) забезпечують приблизний розрахунок значень періодичної функції 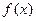 . Для визначення похибки розрахунків за формулами (7.6) і (7.7) застосовується метод оцінки найменшої середньоквадратичної похибка (
. Для визначення похибки розрахунків за формулами (7.6) і (7.7) застосовується метод оцінки найменшої середньоквадратичної похибка ( 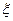 ).
).
Така похибка буде мінімальною 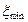 , якщо як коефіцієнти
, якщо як коефіцієнти 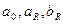 буде використано коефіцієнти Фур’є, які можуть бути представлені таким чином:
буде використано коефіцієнти Фур’є, які можуть бути представлені таким чином:
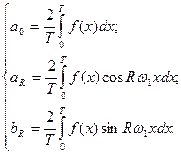 (7.8)
(7.8)
Нескінченний тригонометричний ряд (7) при 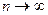 , в якому параметри
, в якому параметри 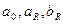 представлені коефіцієнтами Фур’є, називається рядом Фур’є. Періодична функція
представлені коефіцієнтами Фур’є, називається рядом Фур’є. Періодична функція 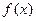 може бути розкладена в ряд Фур’є у тому випадку, якщо її властивості гармонійності відповідають умовам Дирихле. Якщо з практичного погляду розглядати періодичний сигнал
може бути розкладена в ряд Фур’є у тому випадку, якщо її властивості гармонійності відповідають умовам Дирихле. Якщо з практичного погляду розглядати періодичний сигнал 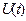 (рис.1), як періодичну функцію
(рис.1), як періодичну функцію 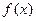 , для якої достеменно виконуються умови Дирихле, то для ряду Фур’є цієї функції наявність властивості сходимості очевидна. Зазначимо, що для досягнення мінімуму середньоквадратичної похибки
, для якої достеменно виконуються умови Дирихле, то для ряду Фур’є цієї функції наявність властивості сходимості очевидна. Зазначимо, що для досягнення мінімуму середньоквадратичної похибки 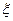 під час використання розрахунків достатньо розрахувати значення декількох перших членів цього ряду.
під час використання розрахунків достатньо розрахувати значення декількох перших членів цього ряду.
Проілюструємо практичне застосування цього теоретичного матеріалу.
Під час проведення процесу діагностування певного блока електронного обладнання, в якому спостерігається відмова ФЕ, контрольний параметр представлений у вигляді сигналу 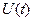 .
.
В такому випадку початковий контрольований сигнал може бути розкладено на окремі гармоніки вигляду 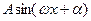 або функції
або функції
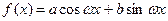 . (7.9)
. (7.9)
Процес класифікації функції на окремі гармоніки, сума значень яких визначається членами ряду Фур’є, носить назву гармонічного або спектрального аналізу.
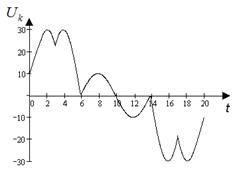
Рис.7.2. Графік зміни величини параметра контролю під час наявності в блоці відмови ФЕ
Враховуючи, що функціонал (7.9) має період 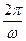 , а також враховуючи умову дотримання властивості частотної циклічності, частоту
, а також враховуючи умову дотримання властивості частотної циклічності, частоту 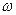 для функції (7.9) вибирають із умови
для функції (7.9) вибирають із умови
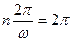 . (7.10)
. (7.10)
З цього очевидно, що 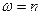 , де
, де 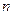 – ціле число.
– ціле число.
Враховуючи викладене і на підставі рівняння (7.7), подамо функцію (7.9) у вигляді ряду:
 (7.11)
(7.11)
Або в скороченому вигляді можна записати:
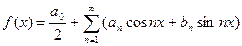 . (7.12)
. (7.12)
В результаті отримали нескінченний тригонометричний ряд при 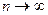 з коефіцієнтами Фур’є
з коефіцієнтами Фур’є 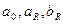 .
.
Таким чином, функція (12) може бути розкладена в ряд Фур’є. Члени зазначеного ряду є простими гармонійними складовими стаціонарного випадкового процесу.
Розглянемо метод застосування гармонійного (спектрального) аналізу для функції стаціонарного випадкового процесу, графічна інтерпретація якого представлена на рис. 7.2.
Із експерименту відомо, що вигляд представленого контрольного сигналу характеризує відмову блока регулювання напруги через причину відмови визначеної сукупності його ФЕ. Необхідно провести спектральний аналіз графічного представлення контрольного сигналу з метою виявлення ФЕ, який відмовив. Якщо такі елементи визначені, їх легко буде замінити, виконавши при цьому відповідні ремонтні роботи.
Для проведення аналізу, на осі  виділимо
виділимо 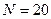 точок через рівні проміжки
точок через рівні проміжки  та побудуємо часовий ряд.
та побудуємо часовий ряд.
Таблиця 7.1.
Часовий ряд значень функції 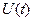
| ||||||||||
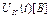
| +21 | +30 | +22 | +30 | +22 | 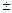 0 0
| +7 | +10 | +8 | 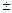 0 0
|
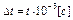
| ||||||||||
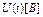
| –9 | –12 | –6 | 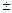 0 0
| –20 | –30 | –20 | –0 | –0 | –0 |
Із часового ряду і представленого графіку зрозуміло, що позитивні й від’ємні значення напруг симетричні відносно абсцис. Тому достатньо провести аналіз для періоду 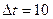 (перших 10 значень).
(перших 10 значень).
Враховуючи дані часового ряду та рівняння (7.12), під час представленого гармонічного сигналу ряд Фур’є буде мати вигляд:
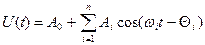 , (7.13)
, (7.13)
де  – постійна ряду,
– постійна ряду, 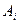 – амплітуда сигналу в і-тій точці графіка,
– амплітуда сигналу в і-тій точці графіка, 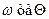 – частота та фаза сигналу; кількість членів ряду
– частота та фаза сигналу; кількість членів ряду 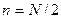 .
.
Тому враховуючи умови (7.8), можна зобразити аналітичні залежності для параметрів рівняння (7.13) так:
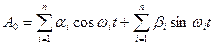 ;
;
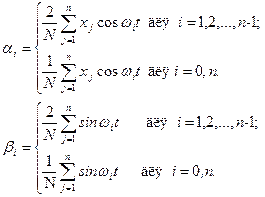
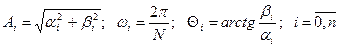 .
.
Дані для 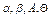 як результат обчислювань заносимо в табл. 7.2.
як результат обчислювань заносимо в табл. 7.2.
Таблиця 7.2
Дані параметрів розрахунку функції U(t)
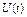
| 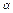
| 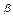
| 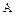
| 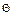
| 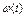
|
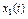
| 8.7 | 9.9 | 0.8 | 0.314 | |
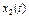
| 6.4 | 6.4 | 8.9 | 0.349 | |
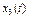
| 0.393 | ||||
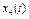
| 0.449 | ||||
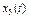
| 0.523 | ||||
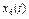
| 0.628 | ||||
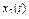
| 0.785 | ||||
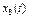
| 1.047 | ||||

| 1.573 | ||||
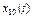
| 3.142 |
Розрахунки та табличні дані показують, що зі складного гармонійного сигналу (рис. 7.2) можемо виділити чотири гармонійні складові (перший, другий, п’ятий та десятий рядок табл.. 7.2) – ті складові, які мають числові значення амплітуди 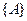 .
.
Згідно з рівнянням (13) отримуємо:
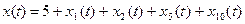 . (7.14)
. (7.14)
В результаті формуємо систему рівнянь:
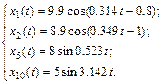 (7.15)
(7.15)
На рис. подамо графічну інтерпретацію кожного з рівнянь системи (7.15).
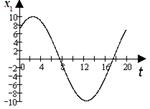
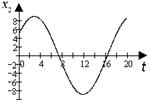
а б
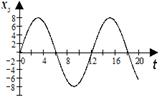
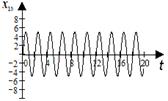
в г
Рис. 7.3. Графіки гармонійних складових контрольного параметра
Результати експериментальних досліджень довели, що в блоці регулювання напруги форма контрольного параметру 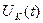 буде мати такий вигляд (подано на рис. 7.2) у разі відмови модуля вимірювання напруги. В самому модулі до такої ситуації однаково призводить відмова таких функціональних елементів, які складають або місток діодів, або місток стабілітронів. Здійснивши спектральний аналіз контрольного сигналу
буде мати такий вигляд (подано на рис. 7.2) у разі відмови модуля вимірювання напруги. В самому модулі до такої ситуації однаково призводить відмова таких функціональних елементів, які складають або місток діодів, або місток стабілітронів. Здійснивши спектральний аналіз контрольного сигналу 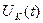 , можна ідентифікувати ті функціональні елементи, які відмовили. Так, графіки функцій
, можна ідентифікувати ті функціональні елементи, які відмовили. Так, графіки функцій 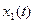 (рис. 7.3а) і
(рис. 7.3а) і 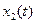 (рис. 7.3б) характеризують відмову містка стабілітронів, а графіки функцій
(рис. 7.3б) характеризують відмову містка стабілітронів, а графіки функцій 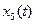 (рис. 7.3в) і
(рис. 7.3в) і 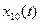 (рис. 7.3г) характеризують відмову містка діодів.
(рис. 7.3г) характеризують відмову містка діодів.
Процедура оцінки технічного стану ЕА методом спектрального аналізу легко автоматизується.
Контрольні питанні
1. Навести ознаки, якими характеризується процес побудови ряду Фур’є?
2. Поясніть в чому полягає сутність процесу розкладання періодичної функції на гармонічні складові?
3. Визначити з яких етапів складається методика практичного застосування засобу перетворення Фур’є?
Література – [2].
Дата добавления: 2020-07-18; просмотров: 783;











