Топологічні моделі для алгоритмізації процесу оцінки технічного стану електронних систем

План лекції

1. Методи та засоби побудови топологічних моделей для функціональних схем блоків ЕА.

2. Сутність процесу оптимізації алгоритму оцінки технічного стану.

3. Топологічні моделі на основі теорії мереж Петрі.

Принципові електричні або електронні схеми сучасної електронної апаратури (ЕА) на практиці реалізовані таким чином, що не завжди для оцінки їх технічного стану можуть бути застосовані методи аналітичного моделювання. Тому часто для побудови ефективних алгоритмів оцінки технічного стану модулів, блоків електронної апаратури застосовують методи топологічного моделювання. У такий спосіб, вирішуються, принаймні, два завдання: контроль працездатності й діагностування (пошук відмов в модулі або в блоці з точністю до функціонального елемента).

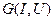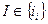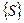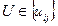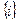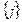Для топологічного моделювання структуру електричних з’єднань ФЕ подають у вигляді графа . Вершини графа зображують множину функціональних елементів. Дуги характеризують шлях між і функціональними елементами. Реалізуючи методики діагностування, враховується рівень працеємності 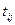доступу до 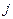-го ФЕ з урахуванням того, що 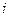-ий ФЕ проконтрольований і за необхідності замінений.

З урахуванням зазначеного завдання діагностування ставиться наступним чином. Для графа 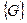, який побудований як топологія з’єднання ФЕ, необхідно визначити мінімальний шлях (алгоритм) діагностування.

Вирішуючи поставлене завдання, необхідно враховувати граничну умову, що під час оцінювання технічного стану існує імовірність помилкової локалізації функціонального елемента. Це призводить до того, що структура алгоритму діагностування не стає оптимальною. Така невідповідність, як правило, враховується у вигляді додаткових витрат при розрахунках рівня працеємності операцій діагностування. Враховуючи викладене, для отримання ефективного алгоритму діагностування необхідно враховувати значення працеємності на кожному із етапів процесу оцінювання технічного стану модулів і блоків ЕА.

Для досягнення необхідного рівня ефективності алгоритму оцінки технічного стану модулів і блоків ЕА застосовується методика, реалізація якої здійснюється за допомогою топологічних моделей зазначених модулів і блоків.

Розглянемо випадок, коли для деякої сукупності ФЕ множини 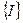у топології графа 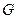існує більше двох шляхів досягнення їх. Тоді виникає невизначеність того, який шлях діагностування виявиться ефективним. Вирішуючи таке завдання застосовують алгоритм Мура, сутність якого така. У графа 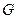вибирається базова вершина 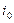. Формується ствердження того, що від вершини 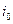і до будь-якої вершини 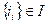існують шляхи діагностування з мінімальними працевитратами тоді й тільки тоді, коли для кожної із вершин 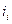існують такі числа-потенціали 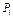, що для будь-якої дуги 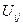графа 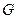, яка з’єднує вершину 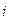з вершиною 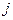, виконується нерівність

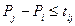(5.1)

Згідно з (5.1), базовій вершині 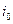надається потенціал 0, а для решти вершин ∞. На кожному із етапів діагностування перевіряють співвідношення

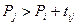(5.2)

І якщо ці співвідношення виконуються, то наступній вершині 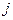надається потенціал, який вираховується як

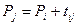(5.3)

В такому випадку вершина 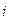вважається попередньою для вершини 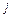в топології шляхів мінімальних працевитрат. Така процедура називається індикацією 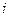-ої вершини. Інформація після проведення зазначених процедур заноситься до банку даних.

Надалі проводиться аналіз інших вершин з погляду їхньої інформативності та рівня працевитрат в алгоритмі діагностування. Вибираються ті вершини, які мають оптимальні характеристики відносно ступеня інформативності і рівня працевитрат, що визначає потенціальний рівень кожної із зазначених вершин. Використовуючи наведену методику, можна визначити не тільки сукупність суттєвих для діагностування вершин, але й оптимальні маршрути пошуку функціональних елементів, які відмовили.

Така методика не є складною у розрахунках, але потребує великого обсягу роботи з підбору різних варіантів досягнення оптимального алгоритму оцінки технічного стану. Для автоматизації процесу реалізації зазначеної методики застосовується топологічне моделювання мережами Петрі. Для вирішення завдання автоматизації подамо мережу Петрі, топологія якої моделює обчислювальну систему.

За свого суття мережа Петрі, яка представлена на рис. 5.1, моделює процес обчислювання за рівняннями (5.1), (5.2), (5.3). Такий процес обчислювання легко програмується для розрахунків на ЕОМ. В результаті отримуємо автоматизований варіант реалізації методики оцінки технічного стану модулів і блоків ЕА.

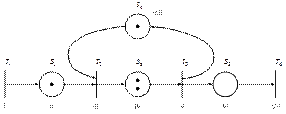
Рис. 5.1. Мережа Петрі як обчислювальна система

Використовуючи мережу Петрі (рис. 5.1), проведемо аналіз алгоритму обчислювання параметрів 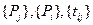. Реалізація такого алгоритму обчислювання в теорії мереж Петрі класифікується як процес маркування вершин мережі. На рис. 5.1 вершини класифікуються як позиції і позначаються через 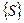. Фішка, яка маркує вершину, позначається міткою (крапкою), (наприклад, як вершини 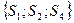на рис. 5.1). Етапи розрахунків на топології позначаються через 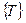і називаються переходами.

Оскільки процес маркування призводить до зміни стану мережі Петрі (топології) 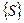, то така процедура адекватна проведенню розрахунків за встановленим алгоритмом. Тому процес маркування мережі Петрі ототожнюється як реалізація функції відображення множини станів 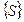у множину деякої сукупності невід’ємних чисел .

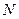Процес маркування 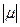визначається розподілом деякої множини маркерів 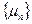на топології мережі. Тоді параметр 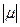представляється вектором

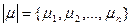, де (5.4)

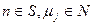– кількість маркерів у вершинах (позиціях) 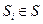. Наприклад, для позиції 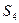– маркер 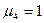, для позиції 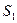– маркер 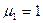, а для позиції 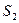– маркер .

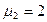На топологічній моделі (рис. 5.1) обчислювання параметрів 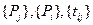здійснюється послідовно за етапами: І – завдання (постановка задачі) поступило на чергу обчислювання; ІІ – завдання очікує; ІІІ – завдання стартує; ІV – завдання обчислюється; V – завдання завершується; VІ – завдання очікує видачі; VІІ – представлення (видача результатів); VІІІ – процесор для розрахунків вільний.

Для практичного застосування топологічних моделей мережами Петрі доцільно знати основні етапи маркування мережі.

Динаміка мережі із одного стану 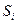в інший 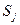здійснюється за дозволом. Перехід 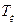вважається дозволеним для проходження логічної операції позиції (вершини) 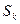тоді і тільки тоді, коли кількість маркерів 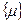цієї позиції не менше ніж кількість дуг, які надходять з інших позицій. Для цього прикладу (рис. 5.1) перехід 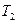буде дозволено в тому випадку, якщо позиція 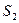буде мати ранг 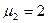, тобто, коли кількість маркерів буде дорівнювати 2, як це подано на рис. 5.1. Це означає, що для реалізації етапу ІV (завдання обчислюється) необхідно, по-перше, мати підготовлене завдання (етап ІІ) і, по-друге, необхідно, щоб процесор (етап ІІІ) був вільний для проведення розрахунків.

Таким чином, кожний із переходів 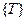може мати два стани: відкритий і закритий. Один стан мережі Петрі відрізняється від іншого залежно від комбінації переходів 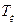. Із викладеного вище слідує, що зміна стану будь-якого із переходів 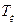призводить до зміни маркування мережі із 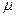на .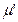

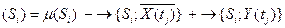. (5.5)

На множині всіх маркувань мережі існує функція переходу одного стану в інший

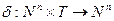. (5.6)

Для оптимізації процесу обчислення з використанням мережі Петрі вводиться критерій досяжності маркування 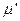. Також стверджується, що маркування 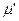безумовно можливе, виходячи із маркування 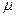, якщо для будь-якого переходу 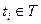існує залежність

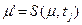. (5.7)

Із зазначеного можна зробити практичний висновок: якщо маркування 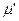досягається із 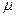, а 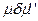, то маркування 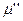досяжне з .

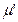У результаті можна дійти висновку про те, що електронну або електричну принципову схему будь-якого блоку ЕА можна подати як топологію системи з’єднання функціональних елементів. Така топологічна модель дозволяє реалізувати на практиці методи оцінки технічного стану блоків (модулів) ЕА. Розглянутий один із ефективних методів топологічного аналізу – це метод мереж Петрі. Відповідно до якого алгоритм оцінювання технічного стану може бути легко автоматизований за допомогою застосування методики маркування мережі Петрі.

Контрольні питання

1. Поясніть, в чому суть методики топологічного моделювання функціональних схем блоків ЕА?

2. Поясніть, які етапи топологічного моделювання мережами Петрі?

3. Поясніть, в чому полягає принцип автоматизації алгоритму оцінки ТС під час застосування теорії мереж Петрі?

Література [5].