Аналіз динаміки та критеріїв сталості перехідних процесів у блоках електронної апаратури

План лекції

1. Постановка задачі дослідження динаміки перехідних процесів в блоках ЕА.

2. Методика аналізу параметрів рівняння перехідного процесу.

3. Визначення основних параметрів для реалізації процедури оцінки технічного стану блоків ЕА.

Постановка задачі. Проводиться процедура оцінки технічного стану певного електронного блоку . Для цього в контрольній точці вимірюється сигнал у вигляді напруги змінного струму. Існують технічні умови для вимірювання зазначеної напруги. Для контрольного сигналу отримані аналітичні вирази як в стаціонарному, так і перехідному режимах роботи електронного блоку.

Використовуючи сучасну електронну вимірювальну апаратуру, необхідно розробити методику вимірювання параметрів стаціонарного і динамічного режимів електронного блока з урахуванням того, що оброблення результатів здійснюється ЕОМ. Процес описаного вимірювання параметрів відповідає процедурі здійснення натурного моделювання процесу оцінки технічного стану об’єкта дослідження. Під час використання моделі рівень ефективності оцінювання параметрів (перевірка моделі на адекватність) здійснюється методом найменших квадратів. Суть полягає в тому, що параметри певної функції, яка описує досліджуваний процес, повинні бути такими, щоб добуток квадратів відхилення теоретичних значень функції від експериментальних був мінімальним.

Наведемо формальну процедуру вирішення поставленого завдання. Нехай деяку функцію представлено виразом:

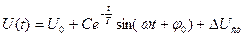, (6.1)

де Т – період коливань, 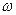– частота, 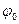–зсув фази, 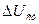– помилка регулювання напруги, 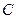– коефіцієнт.

Для рівняння (6.1) потрібно записати функціонал вигляду:

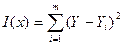, (6.2)

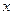– багатовимірний вектор варійованих параметрів, 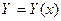– поточне значення вимірюваного параметра, 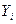– нормовані значення параметрів, 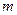– кількість вимірювань.

Задача полягає в знаходженні мінімуму функціонала 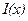(6.2). Нехай 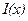– випукла та диференційована функція у всьому Евклідовому 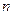-мірному просторі. Необхідно знайти точку 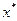мінімуму функції 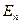у зазначеному просторі.

Виберемо довільне початкове наближення 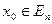та побудуємо послідовність

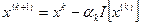, (6.3)

де 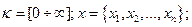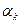– параметричні кроки, які вибираються за умови:

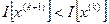. (6.4)

Якщо відбувається наближення градієнта 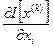до нуля, то визначається умова закінчення розрахунків. Тоді повинна виконуватись нерівність

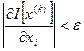, (6.5)

де 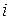– порядкове значення параметрів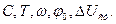

Або

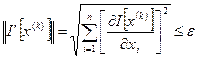, (6.6)

де 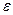– задане достатньо мале число. Використовуючи умови нерівності (6.6), вважають, що

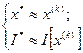(6.7)

Якщо в процесі розрахунків умови нерівності (6.7) не виконуються, тоді крок 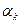зменшують так, щоб умови нерівності (6.4) виконувались, і розрахунки продовжують. Враховуючи викладене, методика аналізу рівняння (6.1) буде такою. Для рівняння (6.2) визначимо

,

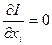де 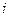= 5 для рівняння (1) ( ).

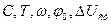В результаті отримаємо систему, що складається з п’яти рівнянь. Запишемо для (2) з урахуванням виразу (1):

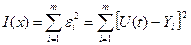(6.8)

Тоді для параметра 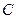із диференційного рівняння (6.1) з частинна похідна буде мати вигляд:

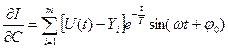(6.9)

Якщо підставимо в (9) вираз (1) для 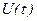та про диференціюємо за 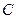, то Отримаємо:

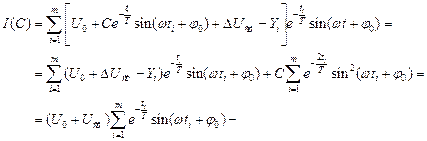
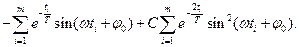(6.10)

Аналогічну процедуру застосовують і для визначення значення параметра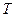

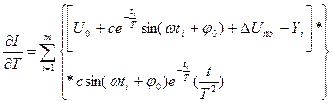(6.11)

Тоді

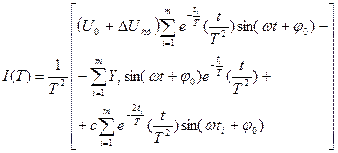(6.12)

За аналогією визначимо вираз для :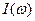

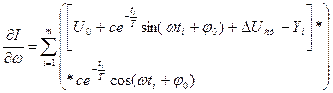(6.13)

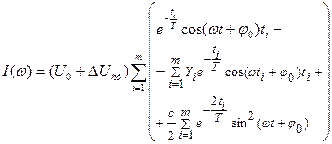(6.14)

Тепер визначимо вираз для :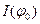

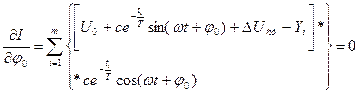(6.15)

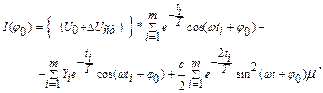(6.16)

Нарешті, визначимо вираз для :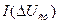

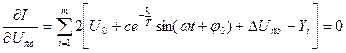(6.17)

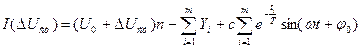(6.18)

Використовуючи наведені аналітичні вирази, можна проводити аналіз технічного стану електронної апаратури як в статичному, так і динамічному режимах функціонування. Для всіх параметрів рівнянь (6.10 – 6.18) фізичні значення можуть бути легко отримані в результаті нескладного експерименту.

Контрольні питання

1. З’ясуйте, з якою метою досліджується динаміка перехідних процесів в блоках ЕА?

2. поясніть, в чому полягає методика знаходження мінімуму функціонала ?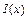

3. Охарактеризуйте, в чому полягає фізичний зміст параметрів ?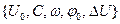

Література – [4].