Анализ возможностей уменьшения целевой функции
Для заключения о возможности дальнейшего улучшения решения необходимо проанализировать вид функции (8.12). Исследование возможности уменьшения целевой функции сводится к анализу строки коэффициентов 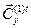 и может дать следующие результаты:
и может дать следующие результаты:
1. Все компоненты вектора  положительны. Это означает, что дальнейшее улучшение целевой функции невозможно и рассматриваемое базисное решение является единственно возможным:
положительны. Это означает, что дальнейшее улучшение целевой функции невозможно и рассматриваемое базисное решение является единственно возможным:  при
при  .
.
2. Некоторые коэффициенты 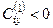 . В этом случае увеличение соответствующих переменных уменьшает целевую функцию. Наибольший эффект будет в том случае, когда выбирается переменная
. В этом случае увеличение соответствующих переменных уменьшает целевую функцию. Наибольший эффект будет в том случае, когда выбирается переменная 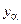 , соответствующая максимальному по модулю отрицательному коэффициенту:
, соответствующая максимальному по модулю отрицательному коэффициенту:  . В алгоритме принимается стратегия, при которой варьируется только одна независимая переменная (движение по грани). При этом все остальные независимые переменные остаются равными нулю.
. В алгоритме принимается стратегия, при которой варьируется только одна независимая переменная (движение по грани). При этом все остальные независимые переменные остаются равными нулю.
Границы изменения 
Увеличение переменной 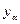 связано с изменением всех зависимых (базисных) переменных (8.10). Некоторые из них будут уменьшаться. Увеличивать переменную
связано с изменением всех зависимых (базисных) переменных (8.10). Некоторые из них будут уменьшаться. Увеличивать переменную  можно лишь до той поры, пока одна из зависимых переменных в системе
можно лишь до той поры, пока одна из зависимых переменных в системе 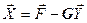 не перейдет через ноль.
не перейдет через ноль.
Поскольку на этом шаге симплекс–метода все независимые переменные за исключением  (это лишь обозначение некоторой реальной переменной
(это лишь обозначение некоторой реальной переменной 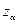 ) равны нулю, то система ограничений может быть представлена в более простом виде:
) равны нулю, то система ограничений может быть представлена в более простом виде:
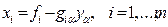 . .
| (8.13) |
Зависимости  показаны на рис. 8.2.
показаны на рис. 8.2.
На рассматриваемом этапе возможны две ситуации:
1. Все  . Увеличение
. Увеличение 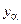 ведет к увеличению всех зависимых переменных (по аналогии с прямой
ведет к увеличению всех зависимых переменных (по аналогии с прямой 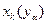 на рис. 8.2) . Поскольку стандартная задача линейного программирования не содержит ограничений по максимальному значению переменных, то
на рис. 8.2) . Поскольку стандартная задача линейного программирования не содержит ограничений по максимальному значению переменных, то  можно увеличивать до бесконечности и целевая функция будет при этом уменьшаться до минус бесконечности. Эта ситуация приводит к окончанию работы симплекс–метода с результатом
можно увеличивать до бесконечности и целевая функция будет при этом уменьшаться до минус бесконечности. Эта ситуация приводит к окончанию работы симплекс–метода с результатом

 .
.
2. Среди компонент 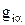 есть положительные. Это значит, что с увеличением
есть положительные. Это значит, что с увеличением  некоторые зависимые переменные уменьшаются и при достижении
некоторые зависимые переменные уменьшаются и при достижении 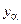 определенной величины первая из них (
определенной величины первая из них (  на рис. 8.2) пересекает ноль, сигнализируя о невозможности дальнейшего увеличения независимой переменной.
на рис. 8.2) пересекает ноль, сигнализируя о невозможности дальнейшего увеличения независимой переменной.
| Рис. 8.2. Поведение зависимых переменных |
Рассмотрим этот случай более подробно. Для этого формируется столбец:
 .
.
Очевидно, что минимальная компонента этого столбца  определяет максимально возможное изменение варьируемой переменной, и номер базисной переменной
определяет максимально возможное изменение варьируемой переменной, и номер базисной переменной 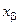 , которая первой пересекает ноль при увеличении
, которая первой пересекает ноль при увеличении 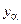 ;
;
Переменная  в дальнейшем не может рассматриваться в качестве независимой переменной. Ее необходимо перевести в класс зависимых переменных. За счет какой другой переменной? Вероятно за счет той, ранее зависимой переменной
в дальнейшем не может рассматриваться в качестве независимой переменной. Ее необходимо перевести в класс зависимых переменных. За счет какой другой переменной? Вероятно за счет той, ранее зависимой переменной  , что стала равной нулю, и которую, возможно, следует увеличить.
, что стала равной нулю, и которую, возможно, следует увеличить.
Совершенно очевидно, что при полученном ограничении 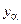 все остальные независимые переменные останутся положительными. Действительно, если подставить значение
все остальные независимые переменные останутся положительными. Действительно, если подставить значение  в систему (8.13), то получим:
в систему (8.13), то получим:
 т.к.
т.к.  .
.
Дата добавления: 2020-07-18; просмотров: 643;











