Конечность алгоритма
Под конечностью любого итеративного алгоритма решения математической задачи понимается возможность получения решения за конечное количество шагов. Симплекс–метод конечен, поскольку здесь выполняется направленный перебор базисных решений, а общее количество базисов для принятой системы ограничений конечно и определяется числом сочетаний из n переменных по m
| Рис. 8.3. Блок – схема алгоритма |
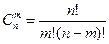 ,
,
где m – ранг матрицы А линейных ограничений (число столбцов больше числа строк), 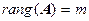 .
.
Обычно симплекс–метод сходится за 3m шагов. Блок– схема симплекс–метода представлена на рис. 8.3
Пример задачи линейного программирования
Требуется найти вектор переменных, минимизирующий линейную функцию
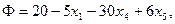
| (8.16) |
при ограничениях
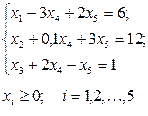
| (8.17) |
Нетрудно видеть, что в системе линейных уравнений переменные 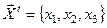 достаточно просто выражаются через
достаточно просто выражаются через 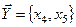 . При этом при
. При этом при 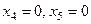 все компоненты вектора
все компоненты вектора 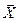 положительны, т.е. определено (первое) допустимое базисное решение:
положительны, т.е. определено (первое) допустимое базисное решение:
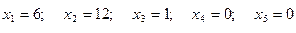 .
.
Замена переменных
Выражаем целевую функцию через независимые переменные 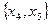
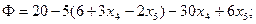
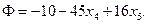
| (8.18) |
Для первого базисного решения Ф=-10.
Анализ коэффициентов целевой функции показывает, что для уменьшения Ф целесообразно снять с нуля переменную 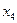 (отрицательный коэффициент). Ищем переменную, которую следует вывести из базиса. Для этого выписываем систему ограничений (8.17) с учетом того, что
(отрицательный коэффициент). Ищем переменную, которую следует вывести из базиса. Для этого выписываем систему ограничений (8.17) с учетом того, что 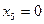 .
.
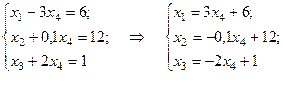
Вектор 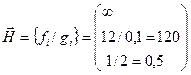 . При увеличении
. При увеличении 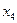 на 0,5 переменная
на 0,5 переменная 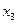 становится равной нулю. Эта переменная выводится из базиса, в то время как
становится равной нулю. Эта переменная выводится из базиса, в то время как 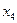 переходит в состав базиса (
переходит в состав базиса ( 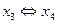 ).
).
Разрешим третье уравнение системы ограничений 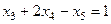 относительно
относительно 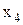
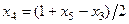
и подставим данное выражение в первое и второе уравнения системы ограничений:
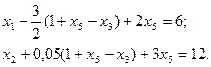
После приведения подобных членов получаем систему ограничений в новом виде:
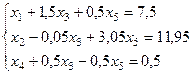
| (8.19) |
Новое допустимое базисное решение (х3, х5 – независимые переменные)
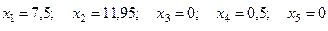 .
.
Выражаем целевую функцию через новые независимые переменные:
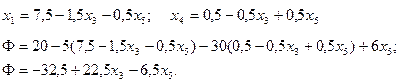
Проще эту операцию выполнять с учетом последнего представления функционала (8.18), где требуется подставить выражение только для одной зависимой переменной 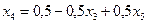 .
.
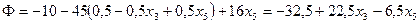 .
.
Анализ коэффициентов целевой функции показывает, что для уменьшения Ф необходимо снять с нуля переменную 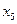 . Выписываем систему ограничений с учетом того, что
. Выписываем систему ограничений с учетом того, что 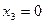 .
.
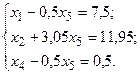
Вектор 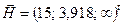 . Переменная
. Переменная 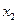 переходит через ноль при
переходит через ноль при 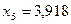 . Ее и следует вывести из базиса: (
. Ее и следует вывести из базиса: ( 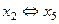 ).
).
Из второго уравнения 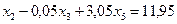 системы ограничений можно получит представление переменной
системы ограничений можно получит представление переменной 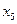
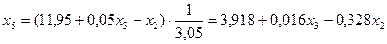 .
.
Данное выражение подставляется в первое и третье уравнения системы (8.19):
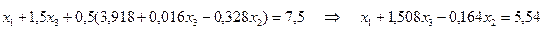 ;
;
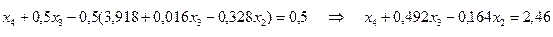 .
.
Новая форма системы ограничений:
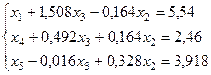
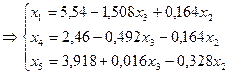
Новое допустимое базисное решение
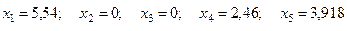 .
.
Выражаем целевую функцию через независимые переменные:
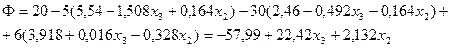
или
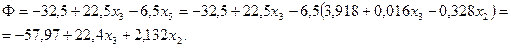
Отсутствие отрицательных коэффициентов показывает, что достигнуто оптимальное значение.
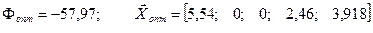 .
.
Дата добавления: 2020-07-18; просмотров: 1334;











