Пример постановки задачи линейного программирования
По критерию минимума затрат на перевозку топлива от угольных бассейнов (шахт) до электростанций (рис. 8.1) необходимо найти оптимальный план топливоснабжения ГРЭС 1, 2, 3 с учетом ограничений по потребностям электростанций, пропускной способности железных дорог и производительности шахт.
Рис. 8.1 Схема расположения ГРЭС и рудников (шахт).
Исходные данные и переменные структурно представлены в табл. 8.2, где:
Lij –длина железнодорожного пути между шахтой i и станцией j (i=1,2; j=1,2,3);
Сij – цена перевозки топлива в направлении от i к j.
Вш1, Вш2 –производительность шахт;
Вc1, Вc2, Вc3 – годовая потребность станций в топливе;
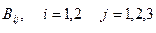искомый объем перевозок;
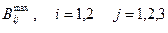- максимальная пропускная способность железной дороги.
Таблица 8.2
| Рудник | Производительность | Электростанции | ||
| Вш1 | L11, С11, B11,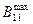 
| L12, С12, B 12,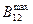 
| L13, С13, B 13,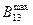 
| |
| Вш2 | L21, С21, B21,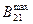 
| L22, С22, B 22,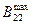 
| L23, С23, B 23,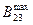 
| |
| Спрос станций | Bc1 | Вc2 | Вc3 |
Поставленную задачу можно сформулировать следующим образом:
Требуется определить оптимальные объемы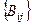 
перевозок топлива от топливных бассейнов (шахт) к пунктам потребления (электростанциям).
Минимизируемой целевой функцией являются суммарные затраты, связанные с перевозкой топлива
 .
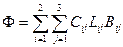| (8.1) |
На переменные 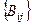накладываются ограничения, формирующие область допустимых значений:
в виде равенств по потреблению топлива станциями (m = 3)
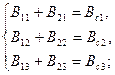
| (8.2) |
в виде неравенств по производительности шахт (r =2)
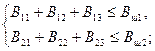
| (8.3) |
системы простых ограничений (ограничения на перевозки по пропускной способности железной дороги)
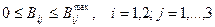
| (8.4) |
Целевая функция (8.1) и система ограничений (8.2)-(8.4) линейно зависят от входящих в них искомых переменных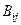 
и вместе составляют задачу линейного программирования.
Дата добавления: 2020-07-18; просмотров: 425;
Поиск по сайту
Узнать еще
- C04 ППВ с комментариями и примерами
- I. Задачи Единой всероссийской спортивной классификации
- II. Цели и задачи службы .
- II. Цель, задачи, приоритеты Стратегии
- III. Биогеохимические циклы элементов и веществ (на примере основных биогенных элементов: углерод, азот, фосфор) и их количественные характеристики.
- III.3.7. ПРЕДМЕТ И ЗАДАЧИ ЛОГОПСИХОЛОГИИ
- IV. Примеры ситуационных задач
- IV.2.7. ПРЕДМЕТ И ЗАДАЧИ ПСИХОЛОГИИ ДЕТЕЙ С ДИСГАРМОНИЧЕСКИМ СКЛАДОМ ЛИЧНОСТИ
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
