Стандартная форма задачи линейного программирования
Любая задача ЛП может быть сведена к своему частному виду, который называется стандартной формой и для которого разработаны эффективные методы решения.
Задача ЛП в стандартной форме не содержит функциональных ограничений типа неравенств (они или отсутствуют, или путем введения новых переменных преобразованы в ограничения типа равенств и простых неравенств). Все простые ограничения этой задачи сводятся к требованию неотрицательности всех переменных.
Таким образом, СЗЛП математически формулируется следующим образом.
Минимизировать функцию цели:
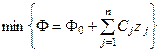 , ,
| (8.5) |
или в матричной форме
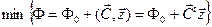
при выполнении условий
ФОР: 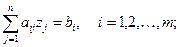 или или 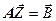 ; ;
| (8.6) |
ПО: 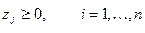 , n >m. , n >m.
| (8.7) |
Относительно уравнений системы (8.6) будем дополнительно предполагать, что они линейно независимы, т.е. не являются следствием друг друга (rang(A)=m). Если это не так, то предварительно решается задача об отыскании в (8.6) максимального числа линейно независимых уравнений, а остальные уравнения отбрасываются как незначимые.
Система уравнений (8.6) может рассматриваться как частный случай решения СЛУ с прямоугольной матрицей при условии выполнения дополнительных ограничений (8.7) . Для решения таких систем используется изложенный в разделе 4.8 общий подход решения СЛУ с прямоугольной матрицей:
Вектор неизвестных 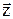 условно можно разделить на две части:
условно можно разделить на две части: 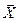 - вектор зависимых переменных с m компонентами и
- вектор зависимых переменных с m компонентами и 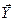 - вектор n-m независимых переменных. СЛУ (8.6) записывается в матричном виде
- вектор n-m независимых переменных. СЛУ (8.6) записывается в матричном виде
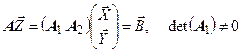
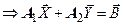 .
.
При этом зависимые переменные выражаются через независимые:
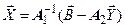 . .
| (8.8) |
С учетом разделения переменных на два класса, 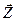 ={
={ 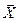 ,
, 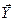 } целевая функция принимает вид
} целевая функция принимает вид
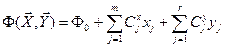 , ,
| (8.9) |
где r=n –m, 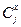 - коэффициенты при зависимых, а
- коэффициенты при зависимых, а 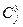 - при независимых переменных.
- при независимых переменных.
Доказано, что решение ЗЛП находится на границе ОДЗ (в вершине или на ребре) Отсюда простейший подход просмотреть все допустимые базисные решения и выбрать то, которое минимизирует целевую функцию. Однако реально приходится иметь дело с задачами достаточно большой размерности, и простой перебор базисных решений может стать недопустимым по времени даже для современных ЭВМ. Более эффективный алгоритм (симплекс-метод), предложен в 1947 году американским математиком Д. Данцигом. Он осуществляет направленный переход от одного допустимого вектора переменных к другому с меньшим значением целевой функции.
Поскольку оптимальное решение задачи ЛП совпадает с базисным решением системы (8.8), для которого вектор независимых переменных равен нулю: 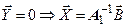 , а процедура поиска решения осуществляется пошаговыми переходами от одного базиса к другому, то в качестве исходного вектора (начальный план) необходимо выбирать любое допустимое базисное решение, удовлетворяющее системе простых ограничений
, а процедура поиска решения осуществляется пошаговыми переходами от одного базиса к другому, то в качестве исходного вектора (начальный план) необходимо выбирать любое допустимое базисное решение, удовлетворяющее системе простых ограничений 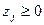 . Получение начального базисного решения составляет специальную задачу ЛП (раздел 8.7).
. Получение начального базисного решения составляет специальную задачу ЛП (раздел 8.7).
Дата добавления: 2020-07-18; просмотров: 655;











