Методы простой итерации и Зейделя-Гаусса для решения СНУ
Применительно к системам нелинейных уравнений методы простой итерации и Зейделя-Гаусса реализуются по тем же алгоритмам, что и при решении линейных систем. Отличие заключается в представлении рекуррентного выражения. Для применения рассматриваемых методов система уравнений 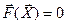 , как и простое нелинейное уравнение, должна быть преобразована к виду
, как и простое нелинейное уравнение, должна быть преобразована к виду 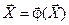 , что позволяет записать рекуррентное выражение
, что позволяет записать рекуррентное выражение 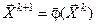 .
.
Пример. Методом простой итерации получить решение УУН в форме баланса токов с заданными мощностями в правой части уравнений. Исходные данные
Uб=10; 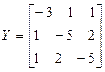 ;
; 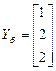 ;
; 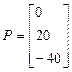 ;
; 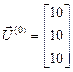 .
.
Рекуррентное соотношение в общем виде
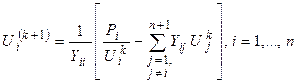 .
.
Рекуррентное соотношение для рассматриваемого примера
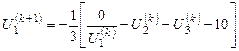 ;
;
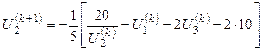 ;
;
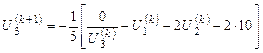 .
.
Первая итерация
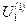 =-
=- 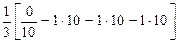 =10;
=10;
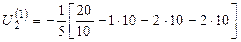 =9,6;
=9,6;
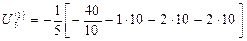 =10,8.
=10,8.
Вторая итерация
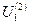 =-
=- 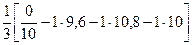 =10,13;
=10,13; 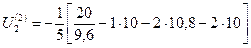 =9,9;
=9,9;
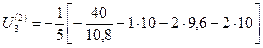 =10,58;
=10,58;
Точное решение 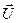 =(10,24; 9,95; 10,77)t
=(10,24; 9,95; 10,77)t
Метод Зейделя-Гаусса отличается от метода простой итерации только схемой вычислений: 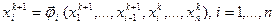 . Критерий сходимости метода Зейделя-Гаусса более сложен. Ускоренный метод Зейделя-Гаусса применяется как и для систем линейных уравнений.
. Критерий сходимости метода Зейделя-Гаусса более сложен. Ускоренный метод Зейделя-Гаусса применяется как и для систем линейных уравнений.
Пример. Выполнить две итерации расчета напряжений предыдущего примера.
На первой итерации U1 и U2 такие же, как и в методе простой итерации. Для третьего узла 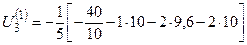 =10,64.
=10,64.
Вторая итерация
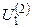 =-
=- 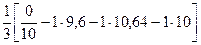 =10,08;
=10,08; 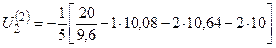 =9,86;
=9,86;
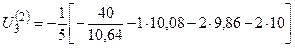 =10,71.
=10,71.
Третья итерация
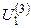 =-
=- 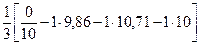 =10,19;
=10,19; 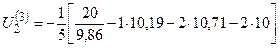 =9,91;
=9,91;
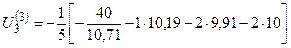 =10,75.
=10,75.
5.3. Критерий окончания расчета при применении итерационных методов
Теоретически итерационные методы дают точное решение при числе итераций, стремящемся к бесконечности. В практике точное решение чаще всего не нужно и можно удовлетвориться некоторым приближением. Кстати, даже прямыми методами нельзя получить точное решение, вследствие ограниченной разрядной сетки ЭВМ и ошибок округления.
Обычно итерационный процесс решения прекращают при выполнении одного условий:
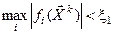 ;
; 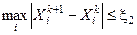 ;
; 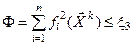 .
.
Дата добавления: 2020-07-18; просмотров: 603;











