Критерий сходимости метода простой итерации
Для того чтобы итерационный процесс метода простой итерации сходился достаточно, чтобы для всех 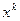 выполнялось условие
выполнялось условие 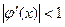 , которое можно рассматривать как критериальное.
, которое можно рассматривать как критериальное.
Для доказательства этого запишем рекуррентные выражения двух соседних итераций 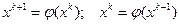 . Отсюда
. Отсюда
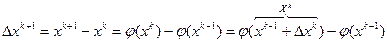 .
.
Разложим функцию j в окрестности 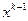 в ряд Тейлора:
в ряд Тейлора:
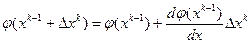 .
.
Отсюда
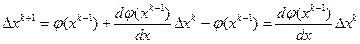 .
.
Для обеспечения сходимости необходимо, чтобы 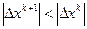 . Это возможно лишь в том случае, когда
. Это возможно лишь в том случае, когда 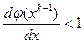 , что и требовалось доказать.
, что и требовалось доказать.
Приведенный анализ показывает основные проблемы итерационных процессов, присущих не только методу простой итерации, но и всем остальным итерационным методам: сходимость или расходимость процесса, критерий и характер сходимости (монотонная, колебательная). Расходящийся итерационный процесс еще не говорит об отсутствии решения. Решение может быть найдено использованием иного математического метода или иной структурой рекуррентного соотношения.
 Пример. Рассмотрим уравнение УУН. соответствующее рис. 6.5
Пример. Рассмотрим уравнение УУН. соответствующее рис. 6.5 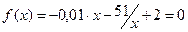 .
.
| Рис. 6.5. Двухузловая схема |
Выражая из первого слагаемого переменную х, получим соотношение: 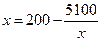 , которое легко представить в виде рекуррентного выражения:
, которое легко представить в виде рекуррентного выражения: 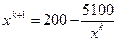 .
.
Примем начальное приближение 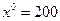 . Тогда:
. Тогда:
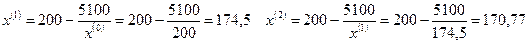 .
.
После семи итераций получается точное решение 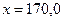 .
.
Легко проверить, что критерий сходимости выполняется, как в точке начального приближения, так и для всех 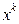 , k=1,2,…, т.к.
, k=1,2,…, т.к. 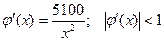 при всех x>71,41.
при всех x>71,41.
Следует отметить, что рассматриваемое уравнение имеет еще один корень 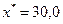 , но получить это решение по представленному рекуррентному соотношению не удается, даже если взять начальное приближение в непосредственной близости от
, но получить это решение по представленному рекуррентному соотношению не удается, даже если взять начальное приближение в непосредственной близости от 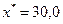 . В то же время, если исходное уравнение записать в виде
. В то же время, если исходное уравнение записать в виде 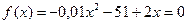 и выразить из этого уравнения
и выразить из этого уравнения 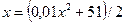 , то соответствующее рекуррентное соотношение
, то соответствующее рекуррентное соотношение 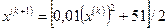 обеспечивает сходимость к корню
обеспечивает сходимость к корню 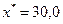 .
.
Дата добавления: 2020-07-18; просмотров: 638;











