Решение системы нелинейных уравнений методом Ньютона
Рассмотрим систему n нелинейных уравнений с n неизвестными:
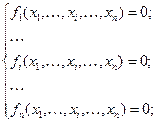
или в виде вектор – функции 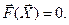
Разложим левые части уравнений в ряд Тейлора в окрестности точки 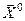 , ограничившись производными первого порядка.
, ограничившись производными первого порядка.

Введем в рассмотрение вектора и матрицы:
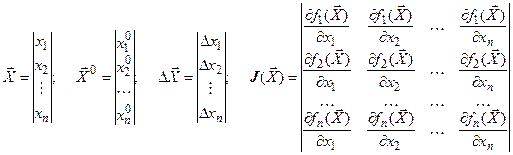
Тогда полученное разложение можно записать компактно в матричной форме:
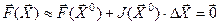 , где
, где 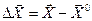 .
.
Матрица 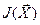 получила название матрицы Якоби. Элемент матрицы Якоби, стоящий на пересечении i-ой строки и j- столбца равен производной от i-го уравнения по j-ой переменной
получила название матрицы Якоби. Элемент матрицы Якоби, стоящий на пересечении i-ой строки и j- столбца равен производной от i-го уравнения по j-ой переменной 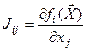 . Матрица Якоби является аналогом производной вектор – функции.
. Матрица Якоби является аналогом производной вектор – функции.
Линеаризация уравнений в окрестности точки 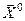 позволяет записать рекуррентное соотношение метода Ньютона
позволяет записать рекуррентное соотношение метода Ньютона 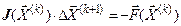 ,
, 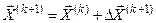 .
.
Пример: Для решения системы УУН, соответствующей рис. 6.2 методом Ньютона выполнить одну итерацию.

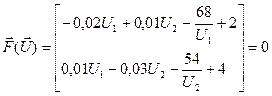 .
.
Матрица Якоби имеет вид:
| Рис. 6.2. Расчетная схема |
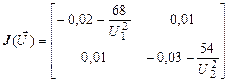 .
.
В качестве начальных приближений примем напряжения узлов равными напряжению базисного узла 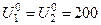 .
.
Вектор функций невязок мощности в узлах
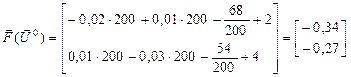 .
.
Матрица Якоби
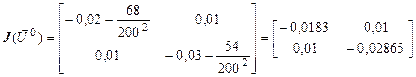
Для получения первого приближения 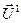 решается система линейных уравнений:
решается система линейных уравнений:
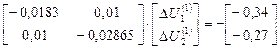 , откуда
, откуда
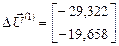 и
и 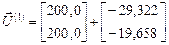 ;
;
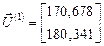 .
.
Для выполнения второй итерации нужно вычислить вектор 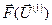 =(-0,0086; -0,0029)t, найти значения матрицы Якоби
=(-0,0086; -0,0029)t, найти значения матрицы Якоби
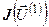 =
= 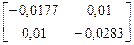
и вновь решить систему уравнений относительно вектора 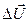 . Здесь
. Здесь 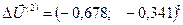 . В результате второй итерации будет получено практически точное решение
. В результате второй итерации будет получено практически точное решение 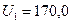 и
и 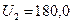 .
.
5.2. Методы простой итерации и Зейделя-Гаусса
Рассмотрим нелинейное уравнение 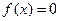 с одной переменной. Для получения рекуррентного соотношения простой итерации его нужно преобразовать к виду
с одной переменной. Для получения рекуррентного соотношения простой итерации его нужно преобразовать к виду 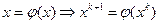 .
.
Ход итерационного процесса можно проследить графически, построив отдельно левую и правую части рекуррентного соотношения. Для произвольно взятого х0 проводится вертикаль до пересечения с 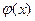 . Значение
. Значение 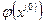 будет принято в качестве х1 . Поскольку функция y=x имеет угол наклона равный 450, то х1 находится как абсцисса точки пересечения горизонтали
будет принято в качестве х1 . Поскольку функция y=x имеет угол наклона равный 450, то х1 находится как абсцисса точки пересечения горизонтали 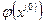 с прямой y=x (рис. 6.3).
с прямой y=x (рис. 6.3).
Возможны следующие реализации итерационного процесса: монотонная сходимость, 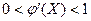 , рис. 6.3, а; монотонная расходимость,
, рис. 6.3, а; монотонная расходимость, 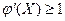 , рис. 6.3, b, колебательная сходимость; рис. 6.4, а; колебательная расходимость, рис. 6.4, b.
, рис. 6.3, b, колебательная сходимость; рис. 6.4, а; колебательная расходимость, рис. 6.4, b.


Рис. 6.3. Метод постой итерации, монотонный процесс : а) 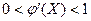 ; b)
; b) 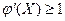


Рис. 6.4. Метод постой итерации, колебательный процесс : а)  ; b)
; b) 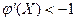
Дата добавления: 2020-07-18; просмотров: 718;











