Нелинейное уравнение с одной переменной
Пусть требуется найти решение нелинейного уравнения 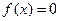 с одной переменной. Функция
с одной переменной. Функция 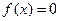 раскладывается в степенной ряд в окрестности точки
раскладывается в степенной ряд в окрестности точки 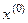 :
:
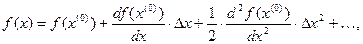
где 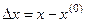 ;
; 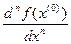 означает, что значения производных функции
означает, что значения производных функции 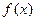 взяты в точке
взяты в точке 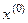 . Если ограничиться двумя членами ряда, то можно найти такое значение
. Если ограничиться двумя членами ряда, то можно найти такое значение 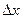 , которое обращает в ноль линейную аппроксимацию исходной функции
, которое обращает в ноль линейную аппроксимацию исходной функции 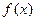 :
:
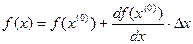 =0
=0 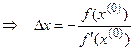 .
.
Это выражение позволяет записать рекуррентное соотношение
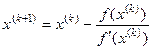 . .
| (6.1) |
На рис. 6.1 представлена графическая интерпретация метода Ньютона. Следующее приближение переменной определяется точкой пересечения касательной к функции f(x) с осью абсцисс.
 Пример. Методом Ньютона получить решение нелинейного уравнения
Пример. Методом Ньютона получить решение нелинейного уравнения 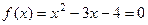 . Точные решения этого уравнения
. Точные решения этого уравнения 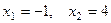 . Однако их требуется найти. Для расчетов методом Ньютона необходимо знать
. Однако их требуется найти. Для расчетов методом Ньютона необходимо знать 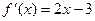 .
.
| Рис. 6.1. Метод касательных |
Решение (3 шага) для двух начальных приближений аргумента (для получения двух корней уравнения) записано в табл. 6.1, 6.2.
Таблица 6.1
| k | 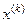
| 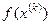
| 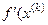
| 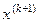
|
| =10-66/17=6,12 | ||||
| 6,12 | 15,07 | 9,24 | 4,48 | |
| 4,48 | 2,66 | 5,97 | 4,04 | |
| 4,04 | 0,2016 | 5,08 | 4,00 |
Таблица 6.2
| k | 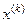
| 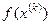
| 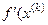
| 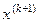
|
| -10 | -23 | -4,52 | ||
| -4,52 | 30,01 | -12,04 | -2,03 | |
| -2,03 | 6,21 | -7,06 | -1,15 | |
| -1,15 | 0,77 | -5,3 | -1 |
Дата добавления: 2020-07-18; просмотров: 636;











