Проблема случайных блужданий
При выводе феноменологических уравнений диффузии из эксперимента определялись макроскопические изменения концентрации, т.е. диффузия рассматривалась как результат статистического эффекта. В своей основе, диффузия есть результат периодических перескоков атомов из одного узла решётки в другой. При этом перемещения атомов в процессе диффузии подчиняются тем же законам, что и броуновское движение. Следовательно, методами математической обработки модели процесса случайных атомных перескоков можно установить связь между макроскопическим коэффициентом диффузии и частотой и длиной перескока. Такая проблема
случайных блужданий впервые была рассмотрена в 1905 году Смолуховским и Эйнштейном.
Была рассмотрена линейная задача (рис. 2.4), в которой атомы могли перескакивать из начальной плоскости ( 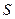 ), в перпендикулярном ей направлении (
), в перпендикулярном ей направлении ( 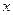 ), на одно и тоже расстояние (
), на одно и тоже расстояние ( 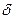 ) с равной вероятностью в обе стороны через равные промежутки времени (
) с равной вероятностью в обе стороны через равные промежутки времени ( 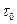 ).
).
|
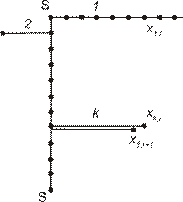
| Рис. 2.4. Схема перескоков атомов при их случайных блужданиях |
Определим размещение атомов после 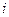 - го и
- го и 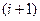 - го скачков. Обозначим расстояние атомов от исходной плоскости
- го скачков. Обозначим расстояние атомов от исходной плоскости 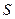 после
после 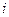 - го скачка через
- го скачка через
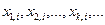 ,
,
а после 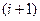 - го скачка через
- го скачка через
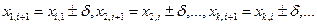
Знаки 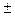 связаны с равной вероятностью скачка как влево, так и вправо. Очевидно, что
связаны с равной вероятностью скачка как влево, так и вправо. Очевидно, что
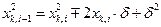 (2.1)
(2.1)
Если число атомов в плоскости 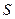 равно
равно 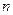 , то среднее значение квадрата смещения атома после
, то среднее значение квадрата смещения атома после 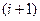 - го скачка запишется как
- го скачка запишется как

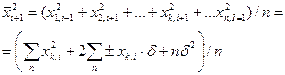 (2.2)
(2.2)
Поскольку 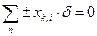 , то запись (2.2) приобретает вид
, то запись (2.2) приобретает вид
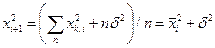 (2.3)
(2.3)
После первого скачка 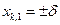 , так что
, так что 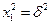 . Тогда
. Тогда 
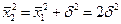 . Для
. Для 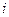 - го скачка
- го скачка
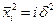 (2.4)
(2.4)
Полученный результат является статистическим, а, следовательно, справедлив только для большого числа частиц и не применим для описания смещения одной частицы. Одна частица после 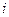 скачков может оказаться как у исходной точки, так и на максимальном расстоянии от неё (
скачков может оказаться как у исходной точки, так и на максимальном расстоянии от неё ( 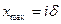 ).
).
Если время процесса отжига обозначить через 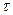 , то число скачков определится как
, то число скачков определится как 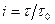 , а частота скачков как
, а частота скачков как 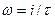 или
или 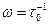 Тогда
Тогда
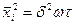 (2.5)
(2.5)
или
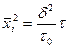 (2.6)
(2.6)
Выражения (2.5) и (2.6) показывают, что диффузионное смещение атома при случайных его блужданиях пропорционально 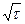 .
.
Вывод для трёхмерного случая аналогичен. В выражение для среднеквадратичного смещения 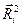 войдёт скалярное произведение радиус-векторов двух последовательных скачков
войдёт скалярное произведение радиус-векторов двух последовательных скачков 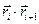 , т.е. произведение их длин на косинус угла между ними (
, т.е. произведение их длин на косинус угла между ними ( 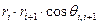 ). При усреднении по ансамблю среднее значение косинуса будет равно нулю.
). При усреднении по ансамблю среднее значение косинуса будет равно нулю.
Установим связь между макроскопическим коэффициентом диффузии 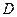 и микроскопическими характеристиками случайных блужданий атомов. Здесь
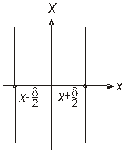
и микроскопическими характеристиками случайных блужданий атомов. Здесь 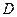 есть коэффициент изотопной диффузии. Рассмотрим линейный случай скачков атомов между двумя соседними плоскостями (рис. 2.5.)
есть коэффициент изотопной диффузии. Рассмотрим линейный случай скачков атомов между двумя соседними плоскостями (рис. 2.5.)
|
| Рис. 2.5. Схема случайных скачков атомов между соседними атомными плоскостями. |
Суммарный поток атомов в положительном направлении 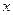 через единицу поверхности в плоскости
через единицу поверхности в плоскости 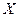 равен разности потоков
равен разности потоков  из плоскости
из плоскости 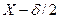 на плоскость
на плоскость 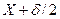 . Эти потоки можно выразить как
. Эти потоки можно выразить как
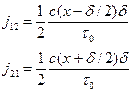 , (2.7)
, (2.7)
где 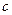 - концентрация или число атомов в единице объёма в плоскости
- концентрация или число атомов в единице объёма в плоскости 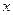 . Множитель
. Множитель 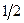 появляется из-за равновероятности скачков в обоих направлениях.
появляется из-за равновероятности скачков в обоих направлениях.
Применим теорему о среднем
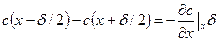 ,
,
тогда суммарный поток 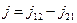 запишется как
запишется как
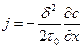 (2.8)
(2.8)
Сравнение полученного результата с первым уравнением Фика приводит к выводу, что
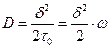 , (2.9)
, (2.9)
а в случае изотропного трёхмерного пространства
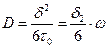 , (2.10)
, (2.10)
в общем случае
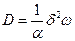 , (2.11)
, (2.11)
где 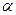 - число разрешённых направлений скачка атома. Для 3-х мерного континуума оно равно 6, т.е. удвоенному числу осей координат. Для кристаллических структур
- число разрешённых направлений скачка атома. Для 3-х мерного континуума оно равно 6, т.е. удвоенному числу осей координат. Для кристаллических структур 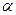 совпадает с координационным числом. Так в ГЦК структуре
совпадает с координационным числом. Так в ГЦК структуре 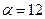 , в ОЦК -
, в ОЦК - 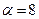 . Параметр
. Параметр 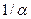 по сути представляет вероятность скачка (
по сути представляет вероятность скачка ( 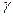 ), поэтому уравнение (2.11) можно переписать в терминах вероятности как
), поэтому уравнение (2.11) можно переписать в терминах вероятности как
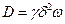 (2.12)
(2.12)
Итак, коэффициент диффузии согласно (2.10) и (2.12) пропорционален вероятности направления, квадрату длины и частоте скачков диффундирующих атомов.
Полученные результаты позволяют рассчитать частоту перескоков диффундирующего атома. Например, для углерода в 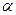 -Fe при 9000С коэффициент диффузии
-Fe при 9000С коэффициент диффузии 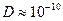 м2/с. Длина скачка соизмерима с периодом решётки, т.е.
м2/с. Длина скачка соизмерима с периодом решётки, т.е. 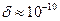 м. Тогда частота скачков
м. Тогда частота скачков 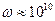 с-1. Дебаевская частота (частота тепловых колебаний) атома составляет 1012-1013 с-1. Таким образом, атом совершает только один скачок за 105-106 колебаний.
с-1. Дебаевская частота (частота тепловых колебаний) атома составляет 1012-1013 с-1. Таким образом, атом совершает только один скачок за 105-106 колебаний.
Интересно сравнить смещение атома в процессе диффузии из исходного положения ( 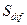 )с общим путём (
)с общим путём ( 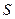 ), который он проходит за время отжига. Для этого воспользуемся формулой (2.5)
), который он проходит за время отжига. Для этого воспользуемся формулой (2.5)
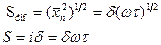
Подставив сюда выше выбранные значения 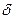 и
и 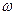 для 100 часового отжига получим
для 100 часового отжига получим 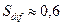 мм, а
мм, а 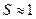 км. Проходя общее расстояние в 1км, атом смещается от исходной точки менее чем на 1мм. Расчёт показывает, насколько мала эффективность случайных блужданий.
км. Проходя общее расстояние в 1км, атом смещается от исходной точки менее чем на 1мм. Расчёт показывает, насколько мала эффективность случайных блужданий.
Эффекты корреляции
При выводе основных соотношений теории случайных блужданий: 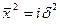 и
и 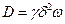 предполагалось, что атомные скачки происходят независимо друг от друга, т.е. между ними нет корреляции: очередной скачок данного атома не зависит от того, каким был предыдущий, и все направления для скачка равновероятны.
предполагалось, что атомные скачки происходят независимо друг от друга, т.е. между ними нет корреляции: очередной скачок данного атома не зависит от того, каким был предыдущий, и все направления для скачка равновероятны.
Однако в реальности последовательные скачки атомов связаны между собой, так что атом совершает не вполне случайные, а скоррелированные блуждания, при которых каждый последующий скачок зависит от того, каким был предыдущий. Это приводит к уменьшению коэффициента диффузии на корреляционный множитель или фактор корреляции. Представление о факторе корреляции было введено Бардиным и Херрингом.
Они показали, что коэффициент самодиффузии, определяемый в экспериментах, отличается от вычисленного в модели случайных блужданий на множитель 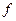 , который они назвали фактором корреляции. Фактор корреляции представляет ту долю скачков, которая вносит эффективный вклад в среднеквадратичное смещение:
, который они назвали фактором корреляции. Фактор корреляции представляет ту долю скачков, которая вносит эффективный вклад в среднеквадратичное смещение:
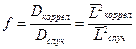 . (2.13)
. (2.13)
В модели случайных блужданий все скачки эффективны, т. е. приводят к диффузионному смещению атома. Однако уже при самодиффузии по вакансионному механизму это не так. Пусть радиоактивный атом на 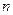 -ном шаге обменялся местами с вакансией. Вероятность повторного обмена с ней же на
-ном шаге обменялся местами с вакансией. Вероятность повторного обмена с ней же на 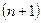 шаге больше вероятности любого другого скачка, поскольку шансов, что среди
шаге больше вероятности любого другого скачка, поскольку шансов, что среди 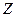 соседей атома имеются сразу две вакансии, ничтожно мало. Между тем при случайных блужданиях вероятность всех скачков должна быть одинаковой. Следовательно, корреляция приводит к тому, что часть скачков оказывается неэффективной. Поэтому фактор корреляции всегда меньше единицы.
соседей атома имеются сразу две вакансии, ничтожно мало. Между тем при случайных блужданиях вероятность всех скачков должна быть одинаковой. Следовательно, корреляция приводит к тому, что часть скачков оказывается неэффективной. Поэтому фактор корреляции всегда меньше единицы.
В первом приближении вероятность того, что атом дважды подряд поменяется местами с одной и той же вакансией и возвратится на прежнее место, в решетке с координационным числом 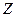 составляет
составляет
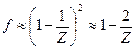 . (2.14)
. (2.14)
Для гцк решетки 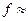 0,83; для оцк
0,83; для оцк 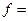 0,75 и т. д.
0,75 и т. д.
Эффект корреляции отсутствует при самодиффузии, т.е. когда решетка состоит из атомов одного сорта, поскольку вакансия движется случайным образом и для неё все атомы одинаковы. Корреляция отсутствует также при самодиффузии для движения атомов по обменному и кольцевому механизмам. В случае прямого межузельного механизма корреляцией нельзя пренебречь, когда доля межузельных атомов достаточно велика или значительная доля междоузлий заполнена - тогда возникает эффект корреляции типа вакансионного. Корреляция существует также для межузельного механизма вытеснения.
С учетом корреляции выражение для коэффициента самодиффузии следует писать в виде
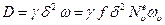 , (2.15)
, (2.15)
где 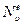 — равновесная концентрация вакансий, а
— равновесная концентрация вакансий, а 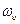 — частота скачков вакансии.
— частота скачков вакансии.
Важно отметить, что величина 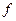 существенно зависит от механизма диффузии.
существенно зависит от механизма диффузии.
Для самодиффузии в кубических кристаллах 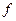 - геометрическая константа, зависящая только от механизма диффузии и структуры кристалла. В некубических кристаллах
- геометрическая константа, зависящая только от механизма диффузии и структуры кристалла. В некубических кристаллах 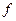 зависит не только от направления в решетке, но также от соотношения частот скачков по разным направлениям.
зависит не только от направления в решетке, но также от соотношения частот скачков по разным направлениям.
Ниже приведены результаты расчета факторов корреляции для самодиффузии в различных кристаллах и по различным механизмам.
| Вакансионный механизм | |
| Структура кристалла | 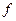
|
| кубическая (типа алмаза) | 0,50000 |
| простая кубическая | 0,65311 |
| оцк | 0,72722 |
| гцк | 0,78146 |
| гексагональная1 | 0,78121*1 |
| и 0,78146*2 | |
| Межузельный механизм вытеснения | |
| простая кубическая*3 | 0,6667 |
| гцк*4 | 0,8000 |
1 Все частоты скачков одинаковы.
*1 Перпендикулярно оси 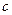 .
*2Параллельно оси .
*2Параллельно оси 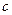 .
*3 .
*3 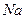 в в 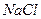 .
*4 .
*4 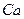 в в 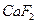 . .
|
При диффузии примеси нельзя даже качественно обсуждать вопрос без эффектов корреляции.
Физически ясно, что при большой энергии связи между вакансией и атомом примеси частота, с которой они обмениваются местами между собой, сильно возрастает по сравнению с частотой обмена вакансии с атомом растворителя. В этом случае вероятность вакансии поменяться местами в разбавленном растворе с одним и тем же примесным атомом очень велика, поскольку остальные её соседи - атомы растворителя, которым вакансия не благоприятствует. Но тогда примесный атом фактически стоит на месте и сдвинется только после того, как вакансия поменяется местами с атомом растворителя. Поэтому среднеквадратичное смещение примесного атома сильно уменьшается по сравнению с рассчитанным в модели случайных блужданий.
При детальном рассмотрении эффекта корреляции для примесных атомов необходимо выразить фактор корреляции через различные частоты скачков, характеризующие обмен местами между вакансией и атомами растворителя и примеси. Если считать раствор разбавленным и учитывать скачки только в первую координационную сферу, то для гцк решетки следует ввести пять различных частот (рис. 2.6) обмена вакансии: 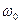 - с атомом растворителя, не являющимся ближайшим соседом атома примеси;
- с атомом растворителя, не являющимся ближайшим соседом атома примеси; 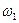 - с атомом растворителя - соседом атома примеси (вакансия была до скачка и остается после скачка соседом атома примеси);
- с атомом растворителя - соседом атома примеси (вакансия была до скачка и остается после скачка соседом атома примеси); 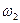 - с атомом примеси;
- с атомом примеси; 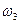 - с атомом растворителя (в результате обмена вакансия уходит от атома примеси, диссоциативный скачок);
- с атомом растворителя (в результате обмена вакансия уходит от атома примеси, диссоциативный скачок); 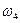 - с атомом растворителя (вакансия становится после скачка соседом атома примеси, ассоциативный скачок).
- с атомом растворителя (вакансия становится после скачка соседом атома примеси, ассоциативный скачок).
Если принять 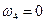 , то
, то
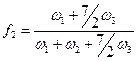 . (2.16)
. (2.16)
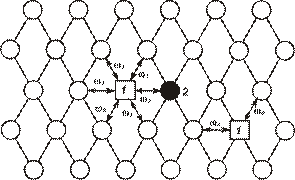
|
| Рис. 2.6. Виды скачков вакансии в кристалле с гцк решеткой: 1 - вакансия; 2 - атом примеси |
Коэффициент диффузии примеси в гцк решетке можно записать в виде 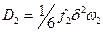 . В данном случае частота скачков атома примеси (
. В данном случае частота скачков атома примеси ( 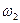 ) представляет собой произведение частоты обмена вакансии с атомом примеси (
) представляет собой произведение частоты обмена вакансии с атомом примеси ( 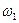 ) на вероятность обнаружить вакансию среди ближайших соседей атома примеси (
) на вероятность обнаружить вакансию среди ближайших соседей атома примеси ( 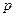 )
)
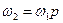 .
.
В кристаллах с ГЦК решеткой 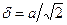 , где
, где 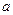 - период решетки, так что
- период решетки, так что
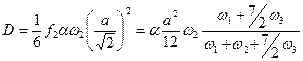 . (2.17)
. (2.17)
Рассмотрим предельные случаи:
1. 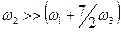 -вакансия значительно чаще обменивается с атомами примеси, чем с атомами растворителя. Это случай сильной корреляции; фактор корреляции минимален, в пределе
-вакансия значительно чаще обменивается с атомами примеси, чем с атомами растворителя. Это случай сильной корреляции; фактор корреляции минимален, в пределе 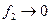 :
:
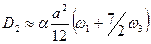 . (2.18)
. (2.18)
Коэффициент диффузии примеси определяется частотой обменов между вакансией и атомами растворителя и не зависит от частоты обмена вакансии с атомом примеси.
2. 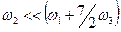 - случай слабой корреляции; в пределе
- случай слабой корреляции; в пределе 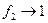 :
:
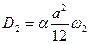 . (2.19)
. (2.19)
Этот результат можно предсказать на основе модели случайных блужданий: коэффициент диффузии определяется частотой скачков примесного атома.
3.Случай самодиффузии. Роль примеси играет атом радиоактивного изотопа: 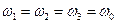 ;
; 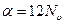 , где
, где 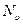 - атомная доля вакансий (
- атомная доля вакансий ( 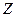 =12 - координационное число гцк решетки)
=12 - координационное число гцк решетки)
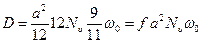 . (2.19а)
. (2.19а)
Таким образом, 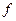 = 9/11 = 0,8181. Для самодиффузии по вакансиям в гцк решетке должно быть
= 9/11 = 0,8181. Для самодиффузии по вакансиям в гцк решетке должно быть 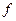 =0,7815. Расхождение - следствие того, что при выводе выражения (2.17) не были учтены ассоциативные скачки (
=0,7815. Расхождение - следствие того, что при выводе выражения (2.17) не были учтены ассоциативные скачки ( 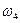 ).
).
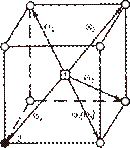
В оцк решетке отсутствует скачок типа 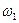 т. е. вакансия, ассоциированная с атомом примеси, не может перейти в другое ассоциированное положение в результате обмена с атомом растворителя, следовательно,
т. е. вакансия, ассоциированная с атомом примеси, не может перейти в другое ассоциированное положение в результате обмена с атомом растворителя, следовательно, 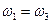 (рис. 2.7).
(рис. 2.7).
|
| Рис. 2.7. Виды скачков вакансии в кристалле с оцк решеткой: 1- вакансия; 2 - атом примеси |
Кроме того, для оцк решеток, видимо; следует учитывать скачки во вторую координационную сферу, так как разница в расстояниях между первыми и вторыми соседями очень мала.
К сожалению, фактор корреляции нельзя найти непосредственно из диффузионного опыта. В металлах его находят из зависимости коэффициента самодиффузии растворителя в растворе от концентрации примеси, либо в результате измерения изотопного эффекта - зависимости скорости диффузионного перемещения от массы диффундирующего атома [5, 9].
Для ионных кристаллов типа 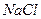 ,
, 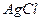 можно найти фактор корреляции, сопоставляя коэффициент диффузии и электропроводность.
можно найти фактор корреляции, сопоставляя коэффициент диффузии и электропроводность.
Дата добавления: 2020-07-18; просмотров: 763;











