Зависимость коэффициента диффузии от температуры

Ранее было показано, что частица совершает диффузионный скачок не чаще одного раза в миллион колебаний, а остальные 999999 колебаний ее положение равновесия не меняется. Это говорит о том, что диффузия является процессом, требующим энергетических затрат, а элементарный акт диффузии связан с преодолением определённого потенциального барьера. Большую часть времени атом находится в равновесном положении, совершая тепловые колебания с малой по сравнению с длиной скачка амплитудой. Диффундирующий атом за счёт тепловых флуктуаций периодически преодолевает барьер и занимает новое равновесное положение в соседнем узле или междоузлии. Так осуществляется диффузионный скачок.

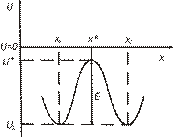
В простейшем варианте рассматривается движение одиночного, свободного атома в одномерном периодическом поле. Потенциальная энергия поля отражает усредненное взаимодействие выделенного атома со всеми остальными атомами кристалла. Для простоты считается, что атом движется в «жестком» потенциальном поле, т.е. все атомы, кроме совершающего скачок, не смещаются из своих положений равновесия. На рис. 2.8. показана энергетическая схема такого движения.

Минимумы энергии на рисунке соответствуют основному состоянию – равновесным положениям атома в кристалле ( 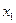, 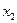и т.д.). Разница между максимальным ( 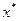) и минимальным ( 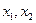) значениями энергии называется энергией активации диффузии (перемещения, скачка).

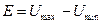
Рис. 2.8. Энергетическая схема движения одиночного, свободного атома в одномерном периодическом поле

Если рассматривать элементарный акт диффузии как скачок изолированного атома, движущегося в усредненном потенциальном поле всех остальных, то к диффузии, вероятно, применимы представления о мономолекулярных реакциях. В существующей у химиков классификации реакций в газовых фазах по молекулярности (мономолекулярные, бимолекулярные), мономолекулярными процессами называют превращения энергетически активированных частиц, которые в момент превращения не взаимодействуют с другими частицами газовой фазы. Такими процессами являются, например, внутренние перегруппировки атомов в молекулах, разрыв связи (диссоциация двухатомных молекул) и т.д. В принципе эта классификация применима и к реакциям в конденсированных фазах.

Для протекания мономолекулярной реакции необходимо, чтобы реагирующая молекула накопила внутреннюю энергию, достаточную для разрыва определенной связи (или связей) или для перегруппировки частиц. Эту энергию, т.е. энергию активации, молекула в газе набирает либо при последовательных «благоприятных» соударениях с другими молекулами газа, либо поглощая кванты света, либо другим путём. При этом активная молекула не обязательно должна диссоциировать. Она может дезактивироваться, отдав избыток своей энергии своим мало энергичным соседям, и чем больше энергия молекулы, тем вероятнее такой процесс. Диссоциация в принципе возможна потому, что интервал между столкновениями велик. При нормальных условиях в газе он составляет порядка 10^-9 с, за это время в молекуле происходит около 10⁴ колебаний. Можно ожидать, что молекула, принимая различные конфигурации, может, в том числе, выбрать такую, которая соответствует энергии, достаточной для разрыва (диссоциации).

Согласно этой простой модели, число элементарных актов разрыва связи в единицу времени (т.н. константа скорости реакции 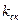) равно произведению частоты колебаний 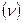на вероятность набрать энергию 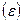, большую энергии активации 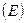. Если молекулы газа подчиняются статистике Больцмана, то указанная вероятность равна 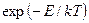и, следовательно

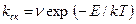(2.20)

За время между скачками в твёрдом теле атом совершает не менее 10⁶ колебаний, т.е. на два порядка больше, чем молекула в газе за время между столкновениями.

Очевидным аналогом числа актов реакции в единицу времени 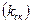является частота атомных скачков 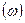. Таким образом:

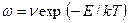(2.21)

и, в соответствии с уравнением (2.11):

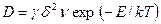, (2.22)

где 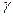- множитель порядка единицы, зависящий от геометрии скачков.

Таким образом, коэффициент диффузии экспоненциально зависит от температуры

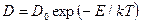, (2.23)

предэкспоненциальный множитель

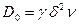, (2.24)

Оценки по уравнению (2.24) дают значение .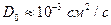

Здесь энергия активации совпадает с высотой барьера, т.е. представляет собой изменение потенциальной энергии атома при переходе из основного состояния (узла, междоузлия) на вершину барьера. Такой подход является во многих случаях достаточным.

Энергия активации в рассмотренной модели является параметром теории. Но теория не дает никаких указаний для оценки высоты потенциального барьера, следовательно, необходимо найти связь между энергией активации 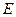и физическими величинами, которые можно определить экспериментально. Кроме того, в рассмотренной модели совершенно не учтено изменение энтропии при переходе атома из узла на вершину барьера.

Для учёта этих можно применить к акту диффузионного скачка теорию абсолютных скоростей реакций или представления о переходном состоянии (активированном комплексе).

Теория абсолютных скоростей реакций или теория переходного состояния была первоначально предложена Эйрингом для расчета скорости химической реакции. Химическая реакция или любой другой протекающий во времени процесс заключается в переходе от начального состояния (начальной конфигурации атомов) к конечному при непрерывном изменении соответствующих координат. Как правило, химические превращения являются «адиабатическими» в том смысле, что потенциальная энергия системы взаимодействующих атомов зависит только от межатомных расстояний. Если построить энергетическую карту реакции, т.е. вычислить потенциальную энергию для всех возможных конфигураций, то превращение должно протекать по некоторому пути вдоль этой поверхности. Всегда есть промежуточная критическая конфигурация, по достижению которой система имеет вероятность, равную единице, дойти до конца превращения. Такая конфигурация называется активированным комплексом или переходным состоянием и соответствует перевальной точке на пути реакции.

Активированный комплекс в теории переходного состояния можно рассматривать как обыкновенную молекулу, обладающую особой поступательной степенью свободы вдоль координаты реакции, что приводит к распаду активированного комплекса.

В такой модели реакция обратима для исходного вещества и активированного комплекса, но необратима для активированного комплекса и продукта превращения.

Исходные вещества 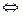активированные комплексы 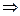продукты превращения.

С помощью статистических методов можно найти концентрацию активированных комплексов 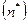и скорость их перехода через перевальную точку, т.е. скорость превращения. Применения этой реакции к атомным скачкам был предложен Вертом и Зинером.

Атом, имеющий три колебательные степени свободы в исходном ( 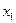) и конечном ( 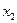) состояниях, в переходном ( 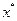) также представляет собой осциллятор, но уже с двумя степенями свободы, колеблющийся в плоскости 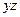, перпендикулярной к направлению скачка. Третья колебательная степень свободы заменяется поступательной, что приводит к появлению для атома вблизи вершины барьера некоторой средней скорости 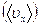в направлении скачка. Предполагается, что потенциальный барьер вдоль пути превращения (рис. 2.8) имеет достаточно плоскую вершину, так что на протяжении малого, но конечного расстояния 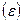потенциальная энергия остается приблизительно постоянной. Атом проходит этот отрезок со средней скоростью 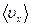, которую можно вычислить из распределения Больцмана:

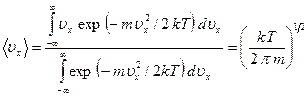, (2.25)

где 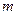- масса атома.

В модели Верта - Зинера фактически сохранена картина индивидуального скачка свободного атома в жестком потенциальном поле, создаваемом остальной решеткой. Потенциальная энергия зависит не только от координат перескакивающего атома 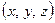, но и его соседей 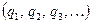, т.е. .

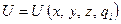Рассматривая не один, а некоторый ансамбль атомов, совершающих скачки - переходы из основного состояния (из узла решетки или междоузлия) в переходное (на вершину барьера), следует учитывать потенциальную энергию группы атомов этого ансамбля. В каждый момент есть равновесие между атомами в исходном состоянии 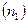и переходном 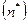, но нет равновесия между переходным и конечным состоянием, что позволяет записать диффузионную «химическую» реакцию в виде:

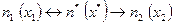. (2.26)

В соответствии с этим скорость реакции ( 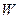) или суммарное число скачков-переходов всех атомов из состояния 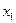в состояние 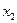в единицу времени определяется числом активированных атомов 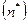в единице объема на отрезке длиной 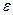, соответствующем переходному состоянию. Все эти атомы, достигшие переходного состояния, неизбежно доходят до конца пути со средней скоростью 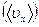на отрезке 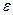в направлении от 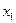к .

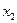Следовательно,

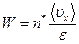. (2.27)

Частота скачков-переходов одного атома

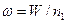
или

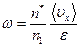, (2.28)

где 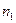- число атомов в единице объема в исходном состоянии (в окрестности ).

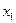Поскольку среднее число частиц в некоторой области фазового пространства пропорционально сумме состояний 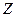в единице объема – функции распределения 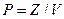, где 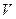- объем. В соответствии с (2.28), атомы в исходном и переходном состояниях находятся в равновесии и можно, воспользовавшись статистической термодинамикой, записать константу равновесия 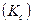в виде

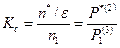, (2.29)

где 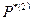и 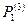- функции распределения атомного осциллятора соответственно в переходном и основном состояниях. Цифры в скобках показывают, что число степеней свободы в этих состояниях различно, т.е. в переходном состоянии одна колебательная степень свободы заменена поступательной.

Полагая, что кинетическая энергия атомов в яме и на вершине барьера одинакова, оставим в выражении для 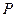только потенциальную энергию, тогда

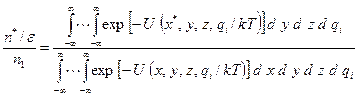. (2.30)

В числители этого уравнения координата перевальной точки 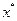фиксирована.

В рассматриваемой модели для основного состояния осциллятора принято гармоническое приближение. Для переходного такое приближение недопустимо, поскольку вблизи вершины барьера потенциал не имеет ничего общего с гармоническим. Разложив 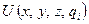в ряд в окрестности 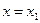, ограничившись квадратичным членом в разложении получим

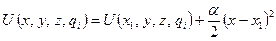. (2.31)

Здесь 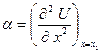- упругая или силовая постоянная. При разложении потенциальной энергии учтено, что .

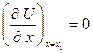После подстановки (2.31) в (2.30) и интегрирования знаменателя получим

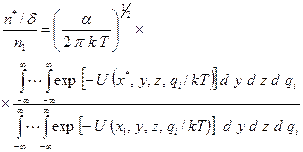(2.32)

Теперь и в знаменателе зафиксирована координата исходного узла 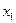. Поэтому

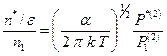. (2.33)

В отличие от уравнения (2.29), в уравнении (2.33) функции распределения в исходном и переходном состояниях соответствуют одинаковому числу степеней свободы. Поэтому можно воспользоваться известным соотношением статистической термодинамики, связывающим функцию распределения ( 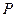) с - изобарно-изотермическим потенциалом системы ( )

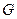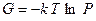(2.34)

и записать

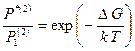, (2.35)

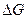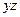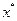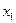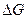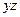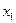где - разница свободных энергий осциллятора, колеблющегося в плоскости в точках с координатами (переходное состояние) и (основное состояние).Другими словами есть работа обратимого изотермического и изобарического перевода атома, свободно колеблющегося в плоскости из в .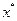

Подставляя выражения (2.25), (2.33) и (2.35) в уравнение (2.21), получим

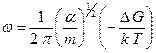(2.36)

или, выражая частоту колебаний через силовую постоянную:

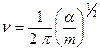(2.37)

и подставляя (2.37) в (2.36):

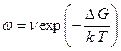. (2.38)

Поскольку

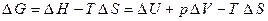, (2.39)

где 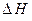, , 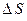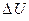и - и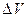зменения энтальпии, энтропии, внутренней энергии и объема при переводе атома из 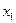в 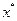; 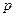- давление, и учитывая, что в соответствии с уравнением (2.19)

,

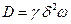получим

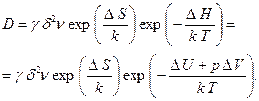(2.40)

Сопоставляя этот результат с уравнением (2.23) можно предэкспоненциальный член записать как

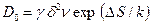(2.41)

а энергию активации представить через энтальпию

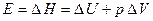. (2.42)

Из данной модели следует, что:

1. коэффициент диффузии экспоненциально зависит от температуры, причем в показатель экспоненты входит не внутренняя (потенциальная), а свободная энергия активации.

2. Энергия активации совпадает с энтальпией активации, т.е. определяется не только изменением внутренней (потенциальной) энергии при переводе атома из основного в переходное состояние, но и активационным объемом, т.е. разницей объемов в этих двух состояниях. Именно активационный объем определяет зависимость коэффициента диффузии от давления

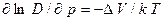. (2.43)

3. Предэкспоненциальный фактор определяется (кроме длины перескока и частоты колебаний) энтропией активации.

Уравнения, полученные с помощью теории переходного состояния, имеют большое значение.

В принципе можно рассчитать параметры диффузии 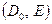теоретически, задаваясь теми или иными моделями переходного состояния. Это позволит получить полезные корреляционные соотношения между энергией активации и термодинамическими параметрами, относящимися только к основному состоянию.

Наиболее важным среди соотношений этой группы являются уравнения, связывающие энергию активации самодиффузии с характеристиками плавления:

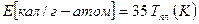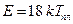или и ,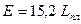

где 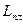- теплота плавления, а 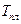- температура плавления.

Поскольку энтропия плавления большинства плотноупакованных металлов есть величина постоянная

,

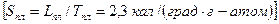то выше написанные уравнения вытекают одно из другого.

На основе оценок работы, совершаемой против упругих сил, удалось установить полезные соотношения между энергией активации диффузии и силовыми постоянными (упругими модулями), сжимаемостью, атомными радиусами, дебаевской температурой.

Например, из рис. 2.9. видно, что, когда внедренный атом (диаметр 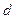) совершает скачок, он должен раздвинуть два атома решетки, находящиеся на расстоянии 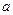, в результате чего возникает деформация

,

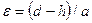где 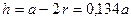, 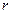- радиус атомов решетки.

Слева показано нормальное положение атомов (положение внедрения характеризуется двумя размерам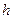и и 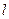), а справа – искаженная конфигурация в плоскости (110) в о.ц.к. решетке.

Рис. 2.9. Искажение оцк решетки при скачке внедренного атома

Результаты расчета упругой энергии деформации в этой модели в сопоставлении с энергией активации диффузии некоторых примесей внедрения приведены в табл. 2.1.

Таблица 2.1 Сравнение экспериментальных значений E с теоретическими для твёрдых растворов внедрения
Растворитель	Примесь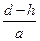
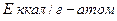
расчетное	опытное
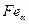
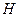
		0,077	1,3	2,9
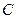
	0,406		19,8-24,6
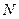
	0,364		18,6
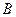
	0,406		-
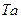
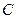
		0,338		38,5
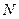
	0,298
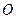
	0,267		25,5
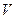
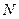
		0,334
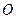
	0,302
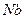
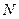
		0,298		34,2
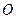
	0,267		26,9

Для углерода и азота в 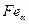значение 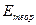примерно на 20% больше 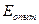, то же самое для углерода, азота и кислорода в тантале. В остальных случаях соответствие хуже. Тем не менее, работа упругой деформации дает существенный вклад в 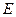. Энергия активации растет с увеличением диаметра внедренного атома.

Очень полезным оказался предложенный Зинером метод расчета 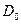, так же основанный на упругой модели. Расчет требует знания энергии активации и поэтому является полуэмпирическим.

В уравнении уравнения (2.41) под экспонентой присутствует энтропия. Так как

,

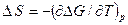то и для энтропии активации можно написать:

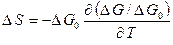. (2.44)

Здесь 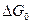представляет собой изменение свободной энергии перемещения при температуре, равной абсолютному нулю 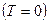. Так как при 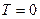член 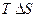обращается в нуль, то 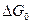в уравнении (2.44) совпадает с энергией активации процесса.

Зинер предположил, что 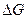состоит только из работы упругой деформации решетки при скачке атома:

,

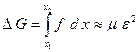где 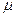- модуль сдвига, а 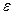- относительная эффективная упругая деформация решетки. Тогда зависимостью модуля сдвига от 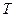запишется как

,

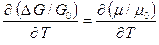откуда

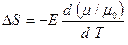. (2.45)

Модуль сдвига уменьшается с ростом температуры, поэтому из теории следует, что .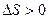

Удобно ввести безразмерный коэффициент

,

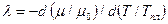теперь

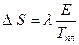. (2.46)

Для большинства металлов .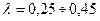

Таким образом, из уравнений (2.41) и (2.46) следует, что

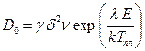, (2.47)

Следовательно, между 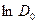и 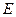должна быть линейная связь, что очень часто наблюдается из экспериментов.

Основное принципиальное возражение против теории переходного состояния заключается в том, что для определения термодинамических свойств переходного (активированного) состояния (его энергии, энтропии, объема и т. д.), оно должно существовать достаточно долго по сравнению со временем полной термической релаксации решетки в некотором объеме в окрестности перевальной точки. Иначе говоря, атом должен пробыть на вершине барьера достаточно долго, чтобы успело установиться равновесие с остальной решеткой. Нет прямых доказательств того, что это условие выполняется. Есть только оценки средней длительности 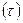случайного «всплеска» энергии (большего энергии активации) на одной из взаимодействующих между собой частиц кристалла в зависимости от структурных характеристик (координационное число, объем и число степеней свободы элементарной ячейки) и дебаевской температуры кристалла. Они показали, что за время 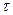к атому, преодолевающему потенциальный барьер, успевает подойти энергия из объема, намного превосходящего объем элементарной ячейки.

Переход атома из потенциальной ямы на вершину барьера в теории переходного состояния обратим. Необратимость вводят чисто формально, заменяя одну степень свободы колебательного движения поступательной в направлении скачка, что соответствует отсутствию равновесия между переходным состоянием и «продуктами реакции». Возможно, что отклонения от равновесия, вызванные отличным от нуля градиентом концентрации, не настолько велики, чтобы повлиять на уравнения, выведенные для равновесия. Однако ясно, что это не всегда так; в частности, вызывает серьезные опасения случай, когда присутствуют другие градиенты, например, градиент температуры. Если же необратимость становится существенной, то можно ожидать, что настоящая теория окажется неприменимой. К сожалению, надежные критерии применимости отсутствуют.

Значительный прогресс в учете коллективного характера диффузионного скачка был достигнут в динамических теориях. Существенно новый элемент, появляющийся в динамических моделях, заключается в. том, что смещение каждого атома из стабильного положения в решетке рассматривается как результат суперпозиции большого числа независимых нормальных колебаний (бегущих волн). Поскольку в каждом нормальном колебании принимают участие все атомы решетки, коллективность достигается автоматически.

В динамических моделях сохраняется концепция критического смещения. Полагают, что скачок произойдет при совпадении двух событий: смещение рассматриваемого атома достигнет критического значения и одновременно его соседи образуют «дыру», т. е. займут положения; благоприятствующие скачку. При этом смещения соседей, даже ближайших, при образовании «дыры» значительно меньше, чем у атома, совершающего скачок, соответственно «дыра» образуется чаще, чем атом в нее смещается.

Таким образом, скачок - результат такой флуктуации в решетке, при которой один атом приобретает большую амплитуду смещения в нужном направлении, а окружающие атомы раздвигаются и дают ему дорогу, так что он может перескочить в соседний узел, не вызывая очень большого увеличения потенциальной энергии решетки.

Никаких ограничений на время перескока этот подход не накладывает.

Что же касается критического смещения, то для большинства металлов с плотноупакованной кубической решеткой (гцк, оцк) хорошее совпадение с экспериментом получилось при величине критического смещения около 30% пути до перевальной точки.