III. Эквивалентное преобразование сопротивления.
Эквивалентным называют такое преобразование части схемы, при котором токораспределение в схеме, не подвергнутое преобразованию, остаётся неизменным.
1. Последовательное соединение сопротивлений.

E I
I
Это соединение, при котором ток через любое сопротивление в любой момент времени одинаков.
E = IR1+ IR2+ ...+ IRn
Мощность, потребляемая цепью не измениться, если все сопротивления заменить их эквивалентными, равными сумме I(R1+R2+...+Rn)=IRэ
2. Параллельное соединение сопротивлений.

I
I I I
E R1` R2 Rn
По первому закону Кирхгофа: I= I1+I2+I3+...+In
Выразим токи данной цепи через параметры схемы:
E/Rэ= E/R1+ E/R2+...+E/Rn
Параллельное соединение сопротивлений называют такое соединение, при котором напряжение на всех сопротивлениях одинаково.
Следствие из первого з-на Кирхгофа 1/R= 1/R1+1/R2+...+1/Rn
Эквивалентная проводимость схемы с параллельными сопротивлениями равна сумме проводимости отдельных параллельных ветвей.
Gэ= G1+G2+...+Gn где G=1/R
Если параллельно соединены 2 сопротивления, то 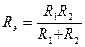
Если параллельно соединены одинаковые по номиналу, то Rэ=R/2
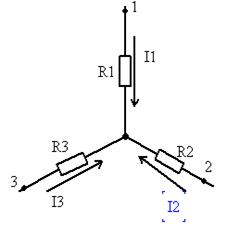
3. Преобразование сопротивлений, соединённых треугольником в соединение звездой.

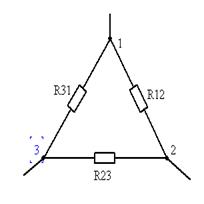
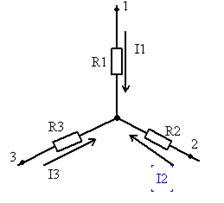
Правило эквивалентных преобразований:
I1тр=I1зв
I2тр=I2зв
I3тр=I3зв
Возьмём и поместим звезду в треугольник, тогда:
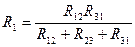
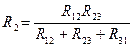
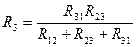
Обратное преобразование из звезды в треугольник:

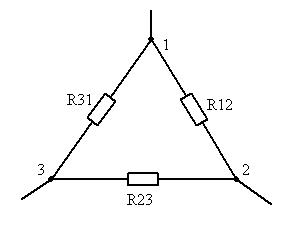
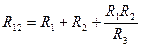
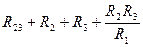
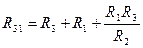
Например:
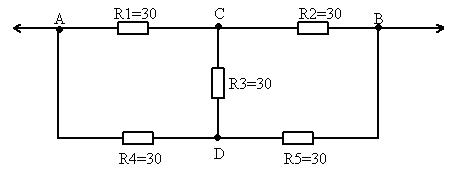
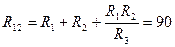 Ом
Ом
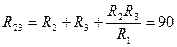 Ом
Ом
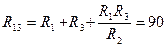 Ом
Ом
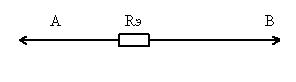
В результате получили схему:
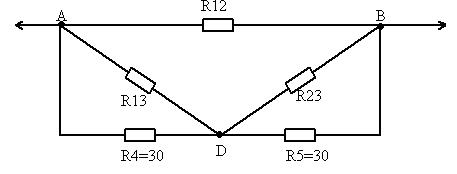
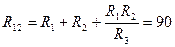 Ом
Ом
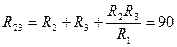 Ом
Ом
 Ом
Ом
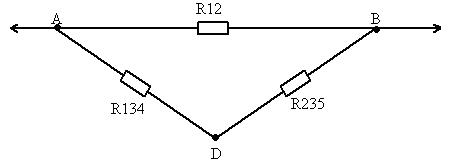
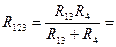 2,25 Ом
2,25 Ом 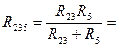 2,25 Ом
2,25 Ом
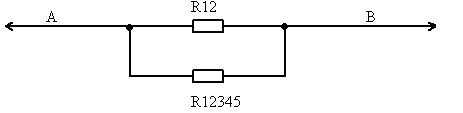
R12345=R134+R235=4,5 Ом
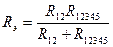
Дата добавления: 2017-09-01; просмотров: 2496;











