Вычисление Z – передаточной функции дискретной системы управления электродвигателем.
Рассмотрим получение уравнений состояния и вычисление передаточной функции для электродвигателя постоянного тока с независимым возбуждением. Уравнения непрерывной части (объекта управления) имеют вид
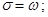
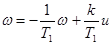
где s - угол поворота выходного вала двигателя; w - частота вращения выходного вала двигателя; u - управляющее якорное напряжение; k - коэффициент передачи двигателя по напряжению; T- электромеханическая постоянная времени двигателя.
Возмущающими воздействиями, действующими на объект управления, пренебрежем. Будем считать, что управление u(t) остается постоянным на интервале квантования 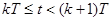
Выберем вектор состояния 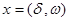 и запишем уравнения объекта в матричной форме:
и запишем уравнения объекта в матричной форме:
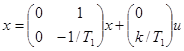
Для вычисления собственной матрицы системы разностных уравнений Ф воспользуемся формулой
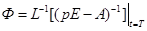
где
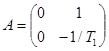
Вычислим обратную матрицу
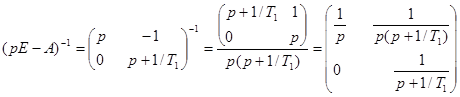
и найдем обратное преобразование Лапласа
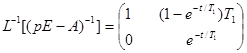
Подставив в последнее равенство t=T , получим собственную матрицу система разностных уравнений:
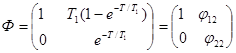
где
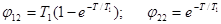
Для определения элементов матрицы Н найдем решение дифференциальных уравнений объекта при нулевых начальных условиях и u=1
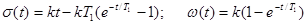
Подставив в полученные зависимости t=T , найдем матрицу H :
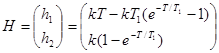
Система разностных уравнений, описывающая поведение объекта при выбранных переменных состояния, будет иметь вид
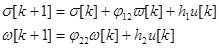
Примем за выходную переменную угол поворота вала двигателя, т.е. 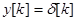 . При этом матрицы С и D преобразуются к виду
. При этом матрицы С и D преобразуются к виду
C=(1,0) ; D=(0)
Тогда выражение для z-передаточной функции будет следующим:
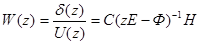
Раскрывая выражения для матриц С, Ф, Н и произведя преобразования, получим
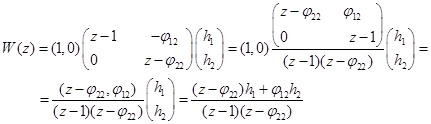
Дата добавления: 2016-07-05; просмотров: 1978;











