Вычисление Z –передаточной функции системы.
Рассмотрим выполнение обратного перехода от уравнений состояния к передаточным функциям системы. Пусть уравнения состояния дискретной системы имеют вид
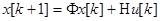 (63)
(63)
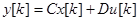 (64)
(64)
где 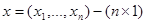 вектор переменных состояния,
вектор переменных состояния, 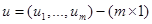 вектор входных воздействий,
вектор входных воздействий, 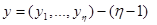 вектор выходных переменных.
вектор выходных переменных.
С другой стороны, система может быть описана матричной Z -передаточной функцией, устанавливающей связь между входными и выходными переменными. Найдем Z -передаточную функцию.
Введем Z -преобразования:
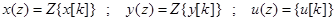
Применяя Z -преобразование к обеим частям уравнений (63),(64), найдем
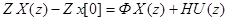 ;
; 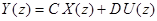
откуда получим
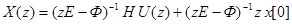
и тогда
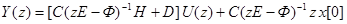
При нахождении передаточных функций полагаем начальные условия нулевыми, x[0]º0. С учетом этого имеем
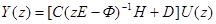 (65)
(65)
Из уравнения (65) получим выражение для матричной передаточной функции дискретной системы в виде
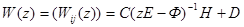
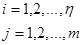
Матричная передаточная функция имеет размерность (h*m), элемент 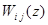 представляет собой передаточную функцию, связывающую j вход и i выход.
представляет собой передаточную функцию, связывающую j вход и i выход.
Раскрывая выражение для матричной передаточной функции, получим
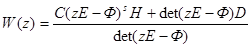
где 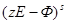 - присоединенная матрица (напомним, что это транспонированная матрица алгебраических дополнений элементов исходной матрицы).
- присоединенная матрица (напомним, что это транспонированная матрица алгебраических дополнений элементов исходной матрицы).
Из последней зависимости видно, что полюсы передаточной функции W(z) являются корнями уравнения
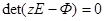
определяющего характеристические числа матрицы Ф. Таким образом, матричная Z-передаточная функция W(z) имеет своими полюсами характеристические числа матрицы Ф.
Алгоритмы получения передаточных функций, основанные на использовании уравнений состояния, удобнее алгоритмов, построенных на формулах 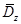 -преобразования. Использование ЭВМ в задачах исследования дискретных систем позволяет применять стандартные программы обращения матриц, что приводит к существенному снижению трудоемкости выполняемых вычислений.
-преобразования. Использование ЭВМ в задачах исследования дискретных систем позволяет применять стандартные программы обращения матриц, что приводит к существенному снижению трудоемкости выполняемых вычислений.
Дата добавления: 2016-07-05; просмотров: 2509;











