Математическое описание синхронных импульсных систем с кратными периодами квантования ИЭ.

Импульсная система может иметь в своем составе несколько импульсных элементов (ИЭ). Наиболее простым является ранее рассмотренный случай, когда у всех ИЭ одинаковые периоды квантования и все они срабатывают одновременно. Такие системы называются синхронными и синфазными. В противном случае говорят об асинхронных (различные периоды квантования) и асинфазных (неодинаковое время срабатывания ИЭ) системах. Математическое описание и анализ таких систем представляют собой сложную задачу, для решения которой можно успешно использовать метод пространства состояний.

Ограничимся рассмотрением асинхронных систем с кратными периодами дискретности импульсных элементов. Такие системы имеют в своем составе непрерывную часть, описываемую линейными дифференциальными уравнениями, и дискретную часть, состоящую из идеальных импульсных элементов (ИИЭ) и формирующих звеньев. Изложим общий подход к математическому описанию данных САУ. Рассмотрим интервал квантования ИЭ и выделим их наименьшее общее кратное Т. Эта величина определяет цикл работы всей системы. Разделим цикл на h подынтервалов в соответствии с моментами срабатывания отдельных ИЭ (рис.38).

Рис.38

На каждом полуинтервале 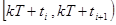в системе можно выделить два типа преобразования вектора состояния:

изменение вектора состояния в интервале между моментами квантования. Эти переходы характеризуются уравнениями вида

,

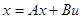где x - вектор состояния; u - вектор управления.

Данному уравнению соответствует решение

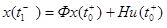(78)

где

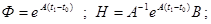
2) изменение вектора состояния в моменты квантования. Эти изменения описываются уравнениями вида

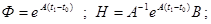(79)

(индексы "-" и "+" соответствуют левым и правым пределам при стремлении аргумента t ).

Осуществляя последовательно переходы (78) и (79), можно установить связь между интересующими нас моментами времени. Например, рассмотрим полуинтервал 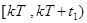. При t=kT имеем переход

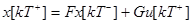(80)

На интервале 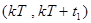имеем переход

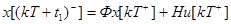(81)

Подставив выражение (80) в формулу (81), получим уравнения, связывающие значения вектора состояния в моменты 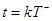и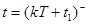

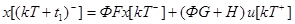
или

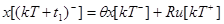
где

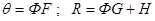
Аналогично рассматриваются и стыкуются между собой последующие интервалы.