Определение переходных процессов при описании дискретных систем уравнениями состояния.

Одной из основных и часто встречающихся задач анализа и импульсных систем является определение переходных процессов. Запишем уравнение (63) импульсной системы в переменных состояния:

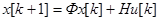
Переходный процесс в такой системе может быть легко найден рекуррентным способом, для систем низкого порядка - непосредственным вычислением, для систем высокого порядка - с применением ЭВМ. Исходными данными для вычислений являются входные воздействия 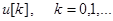, и начальное состояние системы

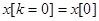
Тогда

и т.д.

Недостатком рекуррентной процедуры является то, что для нахождения решения при определенном значении аргумента необходимо вычислить решение при всех предшествующих значениях аргумента. Поэтому имеет смысл получить решение системы разностных уравнений (63) в явном виде.

Из теории разностных уравнений, которые рассматривались в курсе "Математические основы ТАУ" фундаментальной матрицей однородной системы

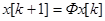(73)

называется 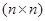- матрица, столбцы которой представляют собой линейно независимые решения системы (73). Фундаментальная матрица x[k] является нормированной при k=0 , если x[0]=E. Общее решение однородной системы (73) имеет вид

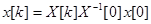(74)

где x[k]- произвольная фундаментальная матрица.

Если x[k]- нормированная фундаментальная матрица, выражение (74) примет вид

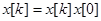(75)

Для определения нормировавшей фундаментальной матрицы применим Z-преобразование к обеим частям уравнения (73):

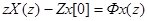
где

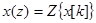
Отсюда следует, что

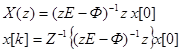(76)

Так как решение линейного разностного уравнения при заданных начальных условиях определяется единственным образом, то из сравнения выражений (76) и (75) будем иметь

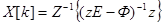
Связь между Z-преобразованием решетчатой функции и оригиналом задается соотношением

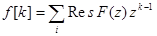
где 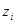- особые точки .

Применив эту формулу для нашего случая, получим

,

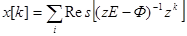где 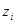- собственные числа матрицы Ф, т.е. корни характеристического уравнения

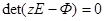
Возможны и некоторые другие способы вычисления матрицы [2].

Перейдем к определению решения неоднородной системы разностных уравнений (63). Получим последовательно

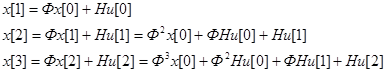
Общее решение неоднородной системы будет иметь вид

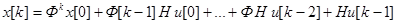
или

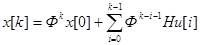
Учитывая, что

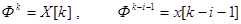
получим окончательное выражение в виде

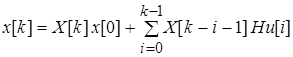(77)

Таким образам, для численного расчета переходных процессов в дискретной системе можно использовать либо рекуррентную процедуру, либо выражения (75), (77). Для изучения общих свойств решения, анализа поведения системы при различных начальных условиях используются формулы (75), (77), характеризующие зависимость переменных состояния от дискретного времени в явном виде.