Динамический критерий устойчивости

Следящие нагрузки

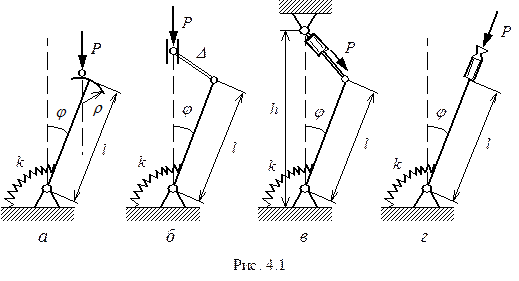
В рассмотренных примерах сила, действующая на систему, сохраняла в процессе отклонения системы как свою величину, так и направление. Такую нагрузку принято называть “мертвой” в отличие от “следящей”, которая зависит от положения системы. Характер приложения нагрузки определяется конструкцией механизма нагружения. Он сказывается на устойчивости системы самым существенным образом.

Рассмотрим несколько различных вариантов приложения нагрузки.

Уравнения равновесия для этих вариантов:

а)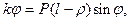

б) 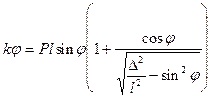, (4.1)

в) ,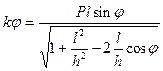

г) .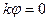

дадут различные значения критических сил. А в варианте а) при 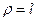и в варианте г) критическая сила отсутствует. Это означает, что возможно только одно вертикальное положение равновесия.

Линеаризованные аналоги уравнений (4.1) дадут ту же информацию о точках бифуркации, что и уравнения (4.1):

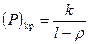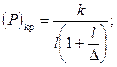
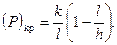; (4.2)

Остановимся подробнее на варианте г), для которого в рассмотренной постановке потеря устойчивости невозможна.

Динамический критерий устойчивости

До сих пор мы говорили о статической устойчивости, понимая под ней состояние, в которое система стремится возвратиться, будучи отклоненной от него неким случайным воздействием. Ясно, что, возвращаясь в положение равновесия, система, вследствие инерционности, будет совершать около него некоторые колебания. Интенсивность этих колебаний (их частота) обусловлена не только соотношением между упругими и инерционными силами (распределением масс в системе), но, кроме того еще и величиной нагрузки. Это можно объяснить следующими рассуждениями.

“Запас статической устойчивости”, под которым можно понимать превышение упругих сил, возвращающих систему к положению равновесия, над возмущающими силами, стремящимися вывести систему из этого положения, по мере приближения системы к критическому значению уменьшается. Это влечет за собой уменьшение частоты колебаний. В момент потери устойчивости, когда запас статической устойчивости исчерпан, возмущающие силы сначала равны восстанавливающим, а затем становятся определяющими. Случайно отклоненная система остается в отклоненном положении равновесия, если такое положение, близкое к исходному, существует, либо устремится к новому равновесия, удаленному от исходного.

Эти соображения позволяют принять характер движения системы за динамический критерий устойчивости.

Если колебания затухают, либо если эти колебания, исследуемые в линеаризованной постановке для системы без рассеяния энергии, оказываются около положения равновесия гармоническими, система устойчива. Если система, выведенная из положения равновесия, удаляется от него или совершает колебания с нарастающей амплитудой, - равновесие неустойчиво. Нагрузки, начиная с которых отклонение или амплитуда колебаний могут увеличиваться, считаются критическими.

Рассмотрим вновь Пример 1.1 но теперь с позиций динамического критерия.

Пусть погонная масса стержня распределена по закону 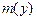. Тогда линеаризованное уравнение движения, в котором кроме упругой и возмущающей силы будут фигурировать также инерционные силы, запишется в виде

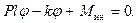(4.3)

Здесь инерционный момент

,

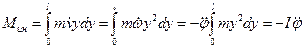где 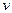- линейная, 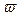- угловая скорости, 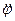- угловое ускорение системы, 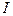- момент инерции стержня относительно опоры, а знак “минус” означает, что система, будучи отпущенной, движется в сторону, противоположную углу, то есть к вертикали.

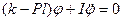. (4.4)

Общее решение этого уравнения при 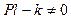имеет вид

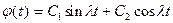(4.5)

или в другой форме записи

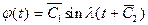, (4.6)

где 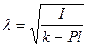, то есть при действительных 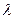и любых константах, определяемых из начальных условий движения, зависимость (4.6) описывает гармонические колебания около вертикального положения равновесия.

При 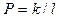уравнение (4.4) вырождается и имеет решение

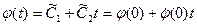. (4.7)

Из (4.7) ясно, что при 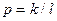система будет либо неподвижна в положении 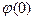, либо при малейшем случайном воздействии, придавшем ей скорость 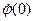, начнет двигаться. Таким образом, мы вновь нашли 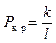, причем, что существенно, эта величина не зависит от 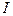, то есть от распределения масс по длине стержня.

Наконец, при 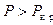, значения 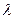становятся чисто мнимыми

,

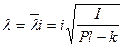и общее решение (4.5) можно переписать в виде

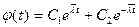
или

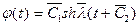. (4.8)

Функции (4.8) при любых константах 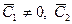описывает движение с экспоненциально нарастающей амплитудой, что соответствует неустойчивому равновесию.

Обратимся к примеру на Рис.4.1г. Линеаризованное уравнение в этом случае

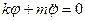
имеет при любых 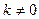, то есть при наличии пружины, решение в форме (4.6). Это означает, что положение равновесия 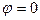всегда устойчиво. Вновь статический и динамический подходы привели нас к одному и тому же результату.

Усложним задачу и рассмотрим систему с двумя степенями свободы.

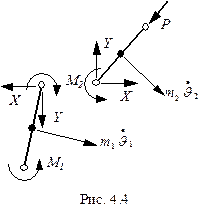
Пример 4.1

Легко видеть, что статическая постановка снова не дает нам иных положений равновесия кроме вертикального, поскольку из положения равновесия верхнего стержня следует, что

,

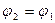то есть стержень не переламывается, и задача сводится к предыдущей.

Чтобы рассмотреть этот пример с помощью динамического критерия, примем (для простоты), что массы стержней расположены в серединах стержней (Рис. 4.3).

Линеаризованные уравнения движения (Рис. 4.4) имеют вид

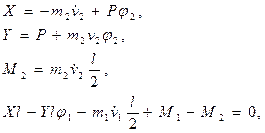(4.9)

где обозначено:

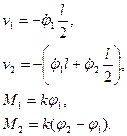(4.10)

Исключив из (4.9) величины Y и X и подставив их в (4.10), имеем

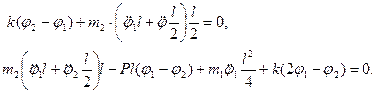
Мы получили систему двух обыкновенных дифференциальных уравнений. Отыскивая ее частное решение в форме

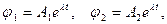(4.11)

приходим к однородной системе относительно констант

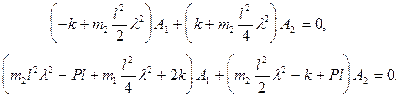
Условие нетривиальности ее решения

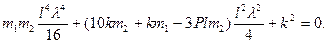(4.12)

Проанализируем уравнение (4.12).

Поскольку свободный член не зависит от , ясно, что нулевых корней 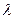нет. Это, означает, что нет независимых от времени положений равновесия (4.11) кроме вертикального 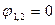. Этого и следовало ожидать. Ведь если бы такое положение было, мы нашли бы его с помощью статического критерия.

Для того, чтобы решение имело расширяющуюся амплитуду, необходимо, чтобы корни уравнения (4.12) в общем случае комплексные

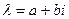(4.13)

имели положительную действительную часть а. Подставив (4.13) в (4.12) и приравняв нулю коэффициенты при действительной и мнимой частях, получим

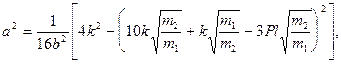
где а - действительный коэффициент. Следовательно, для того, чтобы он существовал, необходимо

.

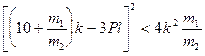Легко видеть, что это вполне возможно. Наименьшее значение , при котором выполняется это неравенство, и будет критическим:

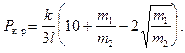(4.14)

Заметим, что на динамический характер потери устойчивости существенно влияет распределение масс.

При 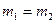имеем .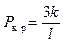

При 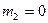из (4.9), (4.10) следует, что 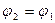, и, следовательно, стержень устойчивости не теряет. По формуле (4.14) этому случаю соответствует .

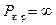Если бы мы учли, что массы стержней не сосредоточены, а распределены, скажем, равномерно, то значение 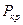за счет появления собственных моментов инерции оказалось бы меньшим [ 3 ]:

.

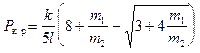Таким образом, динамический критерий в отличие от статического оказывается более общим. Однако, использование этого критерия более трудоемко, и прибегать к его помощи целесообразно лишь тогда, когда статический подход не дает результата.