Псевдочастотные характеристики импульсных систем.

Помимо рассмотренных АФЧХ, для дискретных систем оказывается возможным ввести характеристики, которые по методике построения и по своим свойствам схожи с ЛАФЧХ непрерывных систем. Такие характеристики называются псевдочастотными (ПЧХ).

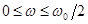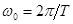Как отмечалось выше, АФЧХ дискретной системы рассматривают в диапазоне частот где - частота квантования. Чтобы использовать привычную методику построения ЛАФЧХ , введем псевдочастоту

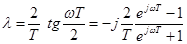. (41)

Зависимость, связывающая w и l, иллюстрируется рис.19, из которого видно, что изменению частоты w в диапазоне 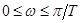соответствует изменение псевдочастоты l в диапазоне .

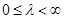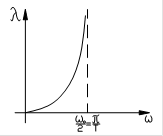Рис. 19

Рассмотрим передаточную функцию дискретной системы . Заменим переменную z на переменную w по формуле

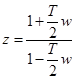(42)

Такое преобразование переменных называется дробно-линейным или билинейным. После замены переменных по формуле (42) передаточная функция преобразуется в передаточную функцию

.

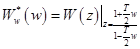Частотные характеристики дискретных систем получают подстановкой в z -передаточную функцию 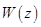величины 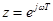. Возникает вопрос, на какую величину следует заменить переменную w в передаточной функции 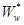, чтобы получить те же частотные характеристики системы.

Из зависимости (42) получим

.

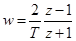При 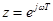, 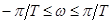имеем

.

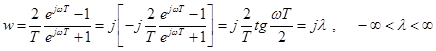Таким образом, частотные характеристики дискретной системы в функции псевдочастоты l могут быть получены заменой в w-передаточной функции 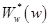переменной w на jl;

.

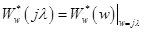Связь псевдочастоты с частотой задается соотношением (41),причем на малых частотах эти величины практически совпадают. Частотная характеристика в функции псевдочастоты l называется псевдочастотной характеристикой.

По отношению к переменной z передаточные функции W(z)-это дробно-рациональные выражения. Следовательно, по отноше­нию к переменной w они также будут дробно-рациональными, т.е. ПЧХ есть дробно-рациональная функция jl , причем l изменяется в пределах от 0 до 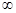. Таким образом, ПЧХ дискретных систем имеют те же асимптотические свойства, что и АФЧХ непрерывных систем.

Наряду с АФЧХ могут быть построены логарифмические псевдочастотные характеристики (ЛПЧХ) дискретных систем. Это позволяет применять известные частотные методы анализа и синтеза непрерывных систем и для дискретных систем.