Методы построения частотных и псевдочастотных характеристик дискретных систем.
Рассмотрим некоторые возможные способы построения АФЧХ дискретных систем. Заметим, что АФЧХ дискретных систем в отличие от АФЧХ непрерывных систем никогда экспериментально не снимаются. Они строятся либо по частотной характеристике ПНЧ, либо по Z-передаточной функции системы W(z) .
Если ПНЧ дискретной системы задана АФЧХ, то АФЧХ импульсной САУ может быть определена по формулам (36), (39).При этом можно либо сначала найти действительную и мнимую частотные характеристики и затем определить 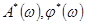 , либо в формулах (36), (39) выполнить непосредственное векторное сложение. Рассмотрим первый способ. Перепишем формулу (39):
, либо в формулах (36), (39) выполнить непосредственное векторное сложение. Рассмотрим первый способ. Перепишем формулу (39):
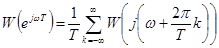 .
.
При известных действительной и мнимой частотных характеристиках ПНЧ P(w), Q(w) получим
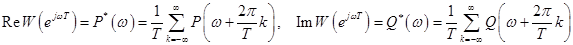 .
.
Обычно в этих соотношениях удается ограничиться конечным небольшим числом слагаемых, что сильно упрощает процесс вычислений. По известным характеристикам 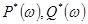 можно построить амплитудно- и фазо-частотные характеристики дискретной системы:
можно построить амплитудно- и фазо-частотные характеристики дискретной системы:
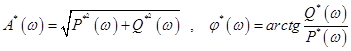 .
.
При непосредственном векторном сложении в правой части равенства (39) удерживается конечное число членов и выполняется их графическое суммирование. Пусть, например, учитываются слагаемые при k=M , -M+1 , …,0,1,… ,M .Тогда получим
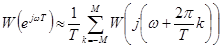 .
.
Кроме изложенных способов для построения АФЧХ дискретной системы может быть использована непосредственно ее Z -передаточная функция W(z). Логарифмические ПЧХ строятся по 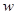 -передаточной функции
-передаточной функции 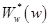 совершенно аналогично тому, как строятся ЛАФЧХ непрерывных систем, с использованием тех же шаблонов для типовых звеньев. При этом возможно использование таблиц
совершенно аналогично тому, как строятся ЛАФЧХ непрерывных систем, с использованием тех же шаблонов для типовых звеньев. При этом возможно использование таблиц 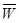 -преобразования [4] ,которое представляет собой результат последовательного применения к передаточной функции W(p) ПНЧ
-преобразования [4] ,которое представляет собой результат последовательного применения к передаточной функции W(p) ПНЧ 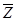 -преобразования и
-преобразования и 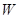 -преобразования.
-преобразования.
Пример. Построить логарифмические ПЧХ импульсной системы, схема которой представлена на рис.20.
 |
Рис. 20
Ранее была найдена z-передаточная функция этой системы:
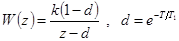 .
.
Выполним подстановку 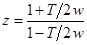 и найдем
и найдем 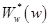 :
:
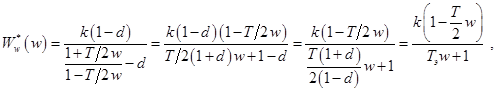
где 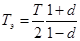 .
.
В числителе полученной передаточной функции 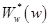 имеется неминимально-фазовое звено, что типично для дискретных систем. Логарифмические ПЧХ данной системы представлены на рис.21. Качественно эти характеристики совпадают с ЛАФЧХ непрерывных систем, что позволяет применить аппарат исследования таких САУ.
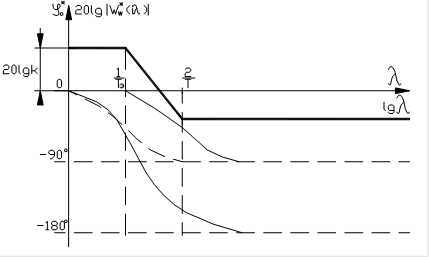
имеется неминимально-фазовое звено, что типично для дискретных систем. Логарифмические ПЧХ данной системы представлены на рис.21. Качественно эти характеристики совпадают с ЛАФЧХ непрерывных систем, что позволяет применить аппарат исследования таких САУ.
 |
При необходимости определения частотных характеристик замкнутой системы по АФЧХ разомкнутой и наоборот, возможно использование номограмм. Отметим, что для схемы, приведенной на рис. 10 , применимы все номограммы, разработанные для непрерывных систем.
Рис.21
Таким образом, для дискретных систем введено понятие частотных характеристик и рассмотрены некоторые способы их построения. С формальной точки зрения АФЧХ дискретных и непрерывных систем совпадают в том, что они характеризуют прохождение гармонического сигнала через систему. Однако следует помнить, что при этом для дискретных систем рассматривался дискретный гармонический сигнал без изучения спектра по непрерывной огибающей. При прохождении непрерывного гармонического сигнала частотные свойства импульсных систем будут существенно отличаться от свойств непрерывных систем.
Дата добавления: 2016-07-05; просмотров: 2367;











