АКФ дискретного сигнала

Важнейшая операция при обработке дискретных сигналов состоит в сдвиге такого сигнала на некоторое число позиций относительно исходного положения без изменения его формы. В качестве примера приведём некоторый исходный сигнал (первая строка) и его копии (последующие строки), сдвинутые на 1,2 и 3 позиции в сторону запаздывания.

…………………………..00011110000……………………………

…………………………..00001111000……………………………

…………………………..00000111100……………………………

…………………………..00000011110……………………………

Обобщим формулу (4.8), чтобы можно было вычислять дискретный аналог АКФ применительно к многопозиционным сигналам. Операцию интегрирования следует заменить суммированием, а вместо переменной 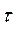использовать целое число n (положительное или отрицательное), указывающее, на сколько позиций сдвинута копия относительно исходного сигнала. Так как в «пустых»позициях математическая модель сигнала содержит нули, запишем дискретную АКФ в виде:

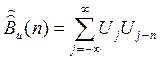(4.15)

Эта функция целочисленного аргумента n естественно обладает многими уже известными свойствами обычной АКФ. Так, дискретная АКФ чётна:

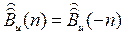(4.16)

При нулевом сдвиге эта АКФ определяет энергию дискретного сигнала:

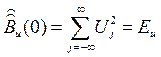(4.17)