Определение установившейся реакции импульсной системы на дискретный гармонический сигнал.
Рассмотрим прохождение дискретного гармонического сигнала
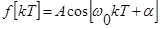 .
.
через импульсную систему с передаточной функцией  . Для этого найдем реакцию системы на воздействие
. Для этого найдем реакцию системы на воздействие
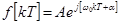 (31)
(31)
и далее выделим ее действительную часть,
Найдем изображение сигнала (31). На основании формулы (20) получим
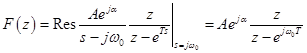 .
.
Изображение выходной переменной системы имеет вид
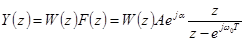 .
.
Вычислив обратное Z-преобразование, найдем реакцию импульсной системы на сигнал (31):
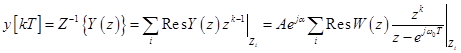
где 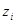 - особые точки выражения, стоящего под знаком вычета, т.е. это полюсы передаточной функции
- особые точки выражения, стоящего под знаком вычета, т.е. это полюсы передаточной функции  и точка
и точка  .
.
Положим для простоты, что полюсы 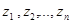 передаточной функции
передаточной функции  некратные и удовлетворяют условию
некратные и удовлетворяют условию
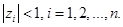 (32)
(32)
Тогда
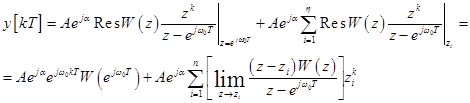
или
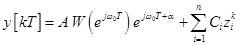 (33)
(33)
где
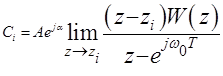 .
.
При выполнении условия (32) второе слагаемое правой части формулы (33) стремится к нулю при 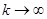 и в системе устанавливается вынужденное движение
и в системе устанавливается вынужденное движение
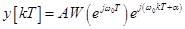 (34)
(34)
Выделив в выражении (34) действительную часть, получим реакцию системы на гармонический сигнал в виде
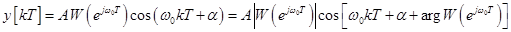 .
.
Из последней формулы видно, что при прохождении дискретного гармонического сигнала через импульсную систему у него изменяются амплитуда и фаза: амплитуда увеличивается в 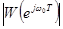 раз, а фаза изменяется на
раз, а фаза изменяется на 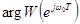 .
.
Дата добавления: 2016-07-05; просмотров: 1818;











