Пример вычисления Z –передаточной функции.

Найдем Z-передаточную функцию разомкну­той системы, состоящей из ИЭ с экстраполятором нулевого по­рядка и непрерывной части с передаточной функцией .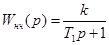

Передаточная функция ПНЧ имеет вид

.

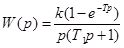Для нахождения W(z) применим формулу (23):

.

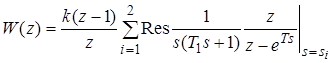Полюсы выражения 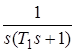следующие: .

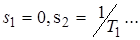Тогда получим

;

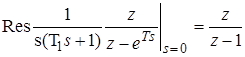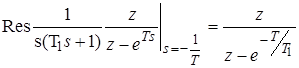
Отсюда следует

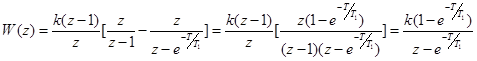
Этот же результат можно получить с помощью таблицы 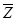-преоб­разования, а именно

.

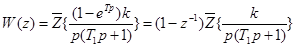Проводя разложение на простейшие дроби, найдем

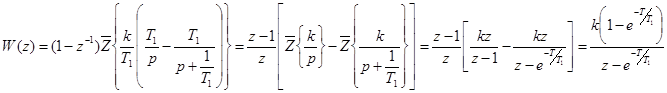
Отметим некоторые свойства Z-передаточных функций. Передаточная функция есть дробно-рациональная функция z. При использовании модифицированного Z-преобразования числитель этой функции зависит от e. Порядком передаточной функции 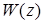назовем степень n ее знаменателя. Порядок дискретной передаточной функции равен степени знаменателя передаточной функции непрерывной части системы .

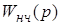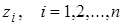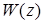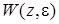Полюсы Z-передаточных функций и связаны с полюсами 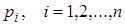передаточной функции 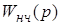непрерывной части и определяются соотношением

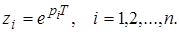(24)

Рассмотрим задачу определения реакции дискретной системы с передаточной функцией 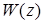на входной сигнал 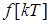. Определив Z-преобразование входного сигнала 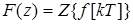, запишем уравнение системы в изображениях:

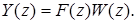(25)

Таким образом, если Z-преобразование выходной величины известно, процесс на выходе может быть найден по формуле обратного Z-преобразования:

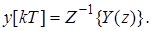
Для нахождения 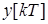можно применить известную формулу

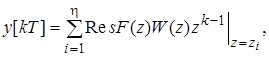
где 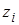- полюсы функций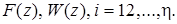

Для вычисления обратного Z-преобразования, кроме того, может быть использовано разложение изображения в ряд Лорана [4]. Наконец, по известной Z-передаточной функции нетрудно составить соответствующее разностное уравнение импульсной системы. Пусть

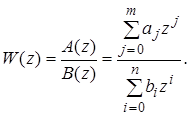
Тогда уравнение (25) можно переписать в виде

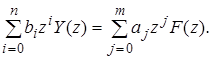
Переходя к оригиналам и учитывая теорему о смещении аргумента решетчатой функции, получим

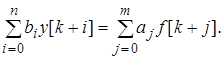
Это соотношение представляет собой разностное уравнение системы, с помощью которого можно рассчитать процесс на выходе дискретной САУ.